1. Quy luật Empirical
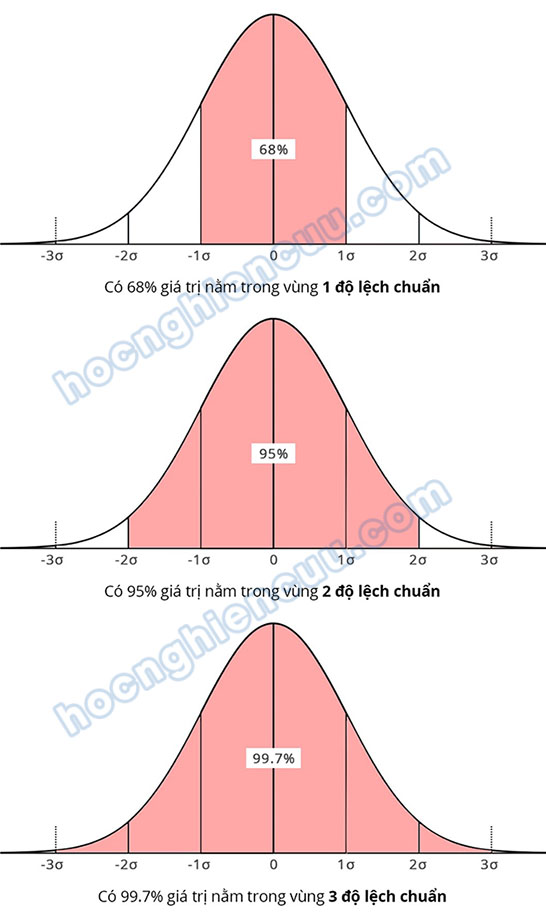
Quy luật Empirical, còn được gọi là quy luật ba sigma hay quy luật 68-95-99.7, quy định rằng đối với phân phối chuẩn, hầu hết tất cả dữ liệu nằm trong ba độ lệch chuẩn (σ – standard deviation) của giá trị trung bình (µ – mean). Theo quy luật này, 68% quan sát nằm trong độ lệch chuẩn đầu tiên (±1σ), 95% quan sát nằm trong hai độ lệch chuẩn đầu tiên (±2σ) và 99.7% nằm trong ba độ lệch chuẩn đầu tiên (±3σ). Trên cơ sở này, nếu tồn tại các điểm dữ liệu nằm ngoài vùng ba độ lệch chuẩn, các điểm dữ liệu đó sẽ được nhận diện là điểm dị biệt.
2. Điểm dị biệt outliers
Điểm dị biệt (điểm ngoại lai – outliers) là những quan sát không nằm trong xu hướng chung so với phần còn lại của dữ liệu. Nếu một bộ dữ liệu xuất hiện quá nhiều điểm dị biệt sẽ làm giảm tính chính xác của các ước lượng thống kê. Cơ chế nhận dạng điểm dị biệt chủ yếu dựa vào tính chuẩn hóa của dữ liệu, các giá trị khác biệt khiến cho dữ liệu giảm khả năng chuẩn hóa sẽ được xếp vào điểm dị biệt cần xem xét. Xét theo tính chất, điểm dị biệt có thể được chia làm hai dạng:
- Loại 1: Điểm dị biệt có thể nhận diện được qua các thống kê tần số, bảng kết hợp do tính bất hợp lý về quy định giá trị hoặc sự logic thông tin. Ví dụ biến giới tính chỉ có hai giá trị được quy định là 1 – nam và 2 – nữ nhưng khi thống kê tần số, biến này lại xuất hiện giá trị ngoài 1, 2. Một ví dụ khác, độ tuổi 18 nhưng thâm niên làm việc là 20 năm, điều này vi phạm sự logic thông tin.
- Loại 2: Điểm dị biệt khó nhận dạng do chúng hợp lý về quy định giá trị, thỏa mãn tính logic thông tin nhưng lệch khỏi xu hướng phân phối chuẩn dữ liệu. Các điểm dị biệt này làm ảnh hưởng đến một số kết quả thống kê định lượng, tùy số lượng điểm dị biệt cũng như mức độ dị biệt mà sự ảnh hưởng là nhiều hay ít.
Nếu xét theo tính kết hợp, thì điểm dị biệt được chia làm hai loại là univariate (dị biệt đơn lẻ) và multivariate outliers (dị biệt kết hợp):
- Univariate outliers là những điểm dị biệt xuất hiện khi xét trong một biến đơn lẻ. Mỗi biến sẽ được phân tích điểm dị biệt một lần. Ví dụ, chúng ta có ba câu hỏi hỏi về giới tính, thâm niên làm việc, sự hài lòng trong công việc, thì ba câu này sẽ phân tích điểm dị biệt tách riêng nhau, không có sự liên quan nào giữa ba câu hỏi. Do đó, kết quả chúng ta sẽ có điểm dị biệt của biến giới tính, điểm dị biệt của biến thâm niên, điểm dị biệt của biến sự hài lòng.
- Multivariate outliers là những điểm dị biệt xuất hiện khi kết hợp hai hay nhiều biến. Ví dụ, khi chúng ta xem xét mối quan hệ giữa thâm niên làm việc và sự hài lòng, sẽ có những điểm dị biệt xuất phát từ sự kết hợp giữa hai biến này với nhau. Điểm dị biệt này có thể trùng với điểm dị biệt đơn lẻ hoặc khác với điểm dị biệt đơn lẻ của mỗi biến.
Việc phát hiện và loại bỏ, điều chỉnh điểm dị biệt là cần thiết, tuy nhiên không được lạm dụng để cải thiện các chỉ số thống kê. Nếu điểm dị biệt mà giá trị của chúng nằm ngoài phạm vi thang đo, hoặc không hợp lý về tính logic thông tin, hoặc thực sự khác biệt quá lớn so với xu hướng chung của dữ liệu chúng ta mới cân nhắc loại bỏ.
Loại bỏ điểm dị biệt thiếu sự xem xét kỹ lưỡng sẽ làm cho cỡ mẫu giảm đi, đồng thời chúng ta cũng đang loại bỏ đi một phần tính thực tế của nghiên cứu. Tuy đó là điểm dị biệt nhưng chúng lại là câu trả lời thực tế của đáp viên, nếu chỉ vì để các chỉ số thống kê tốt hơn mà loại bỏ đi tính thực tế, điều này đã đi trái với mục đích nghiên cứu chúng ta đặt ra. Bên cạnh đó, không phải lúc nào xử lý điểm dị biệt cũng làm mô hình tốt hơn, thậm chí còn xảy ra tác dụng ngược như độ phù hợp mô hình giảm, biến độc lập có ý nghĩa lại trở thành không có ý nghĩa. Do vậy, kỹ thuật này cần thực hiện một cách cân nhắc, thử-sai liên tục để loại bỏ đúng các điểm dị biệt xấu nhằm có được kết quả cuối cùng tốt hơn chứ không phải thu về một kết quả tệ hơn.
Xem tiếp: Nhận diện điểm dị biệt bằng bảng tần số, bảng kết hợp trong SPSS