Ở bài viết Quy luật Empirical và điểm dị biệt outliers trong thống kê, chúng ta đã tìm hiểu về khái niệm cũng như bản chất của điểm dị biệt. Phần nội dung tiếp sau đây, chúng ta sẽ thực hành các phương pháp phát hiện điểm dị biệt trên tập dữ liệu có tên 350 – DLTH 4 – OUTLIER.sav của ebook SPSS 26 Phạm Lộc Blog. Lưu ý, để thực hiện các phương pháp nhận diện và xử lý điểm dị biệt, trong dữ liệu luôn phải có cột biến số thứ tự của quan sát trong mẫu. Cụ thể trong dữ liệu này, biến số thứ tự trùng với ID phiếu khảo sát.
Đồ thị Boxplot là phương pháp phổ biến trong nhận diện điểm dị biệt loại 2 dựa trên đặc điểm phân phối chuẩn dữ liệu trong phân tích thống kê. Đại đa số các kiểm định hoặc phương pháp phân tích đều dựa trên giả định về tính phân phối chuẩn của dữ liệu. Khi dữ liệu đảm bảo giả định phân phối chuẩn, các ước lượng thống kê sẽ tăng tính chính xác, các chỉ số thống kê tốt hơn rất nhiều so với một tập dữ liệu không có phân phối chuẩn. Nguyên nhân dẫn đến phân phối không chuẩn là do sự xuất hiện của điểm dị biệt lệch khỏi xu hướng chung của dữ liệu. Tùy vào mức độ lệch khỏi xu hướng mà điểm dị biệt sẽ được chia thành “outliers” (lệch ít) và “extreme outliers” (lệch rất nhiều). Chúng ta sẽ loại bỏ điểm dị biệt lệch nhiều nhất, sau đó mới loại điểm dị biệt lệch ít. Trong đồ thị boxplot, outliers được ký hiệu bằng hình tròn () và extreme outliers được ký hiệu bằng hình ngôi sao (). Ảnh bên dưới cho thấy quan sát 33 là extreme outliers, các quan sát 7, 17, 26, 191 là outliers.
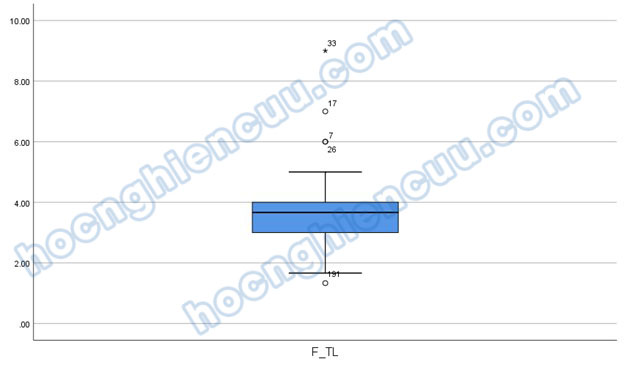
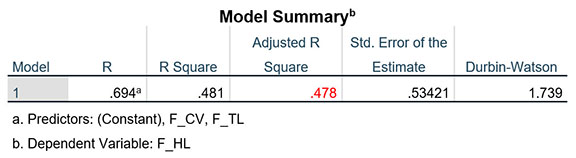
Thực hành với tập dữ liệu mẫu, chúng ta có ba biến F_TL, F_CV và F_HL là biến đại diện được tạo từ các biến quan sát. F_HL là biến phụ thuộc, trong khi đó F_TL và F_CV là hai biến độc lập. Thực hiện hồi quy tuyến tính bội, chúng ta có được giá trị Adjusted R Square trong bảng Model Summary bằng 0.478. Đây là một chỉ số thể hiện mức độ phù hợp của mô hình hồi quy, chỉ số này càng tiến về 1, càng cho thấy mô hình hồi quy là phù hợp.
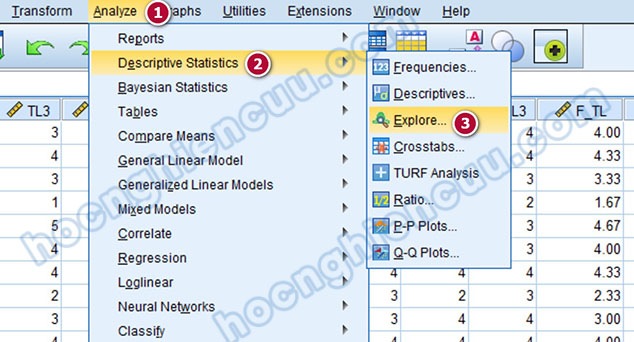
Chúng ta sẽ dùng đồ thị Boxplot để loại bỏ điểm dị biệt trên các biến tham gia vào hồi quy để xem giá trị Adjusted R Square có tăng lên hay không (mô hình có phù hợp hơn hay không). Trong ví dụ bên dưới, tác giả sẽ chỉ loại bỏ outliers trên biến phụ thuộc F_HL để làm mẫu, trên thực tế tùy tập dữ liệu mà chúng ta sẽ xử lý điểm dị biệt trên độc lập, trên phụ thuộc hay cả hai loại biến. Tại giao diện phần mềm SPSS, vào Analyze > Descriptive Statistics > Explore…
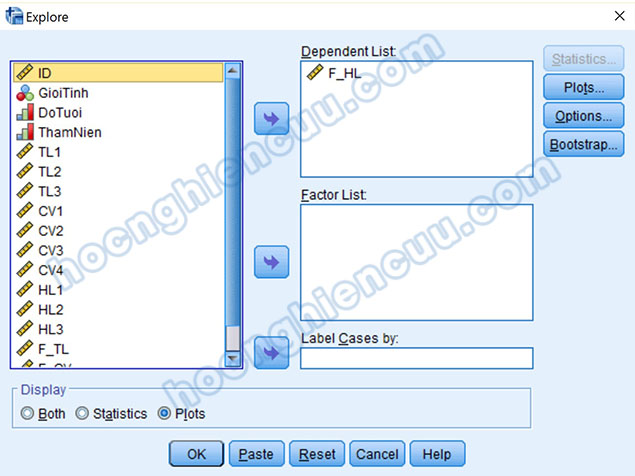
Cửa sổ Explore xuất hiện, chúng ta đưa biến phụ thuộc F_HL vào mục Dependent List để xem xét dị biệt đơn lẻ. Trong trường hợp muốn đánh giá dị biệt kết hợp, chúng ta sẽ đưa các biến muốn kết hợp vào mục Factor List. Giả sử xem xét kết hợp giữa F_TL và ThamNien, chúng ta đưa F_TL vào Dependent List, đưa ThamNien vào Factor List, lúc này phần mềm sẽ xác định điểm dị biệt từ sự kết hợp dữ liệu của hai biến này.
Trong tùy chọn Statistics, chúng ta bỏ chọn ở Descriptives, tích chọn vào Outliers, sau đó nhấp vào Continue để quay lại cửa sổ ban đầu.
Trong tùy chọn Plots, bỏ tích chọn mục Stem-and-leaf. Biểu đồ Stem-and-leaf cũng là một công cụ chúng ta nhận diện điểm dị biệt, tuy nhiên, tài liệu này chủ yếu tập trung vào phương thức boxplot – một phương thức xác định điểm dị biệt được đánh giá cao. Chọn Continue để quay lại cửa sổ ban đầu, nhấp OK để xuất kết quả ra output.
Kết quả cho thấy F_HL có điểm dị biệt outliers và không có extreme outliers. Nên nhớ rằng, những tập dữ liệu có cỡ mẫu lớn luôn tồn tại các điểm dị biệt. Một lần nữa tác giả xin nhấn mạnh, việc loại bỏ điểm dị biệt khỏi nghiên cứu nên được thực hiện một cách thận trọng và mang tính cân nhắc bởi việc làm này có thể sẽ làm mất đi tính thực tế của nghiên cứu cũng như giảm đáng kể kích thước mẫu.
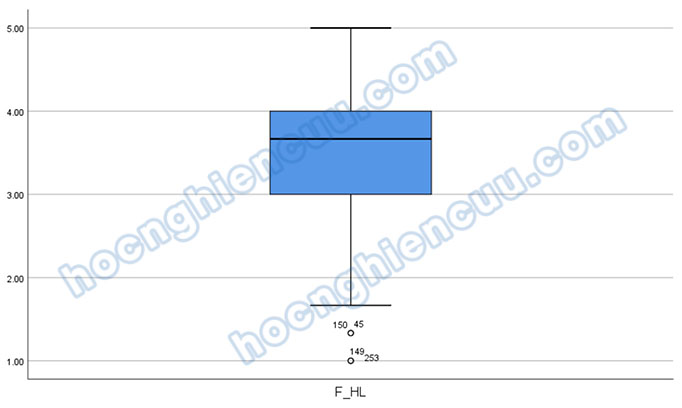
Tác giả sẽ loại bỏ đi các quan sát dị biệt gồm: 45, 149, 150, 253. Không nên xóa bỏ trực tiếp các quan sát dị biệt khỏi dữ liệu phòng trường hợp chúng ta cần dùng lại chúng. Chúng ta sẽ dùng lệnh Select Cases để yêu cầu phần mềm không tính toán các quan sát này. Trong hộp thoại Select Cases: If, chúng ta gõ hàm: ID ~= 45 AND ID ~= 149 AND ID ~= 150 AND ID ~= 250. Trong đó, ID là biến ID trong tập dữ liệu, mỗi quan sát sẽ tương ứng với một ID khác nhau; ký hiệu “~=” mang ý nghĩa là “khác, không bằng”; hàm “AND” mang ý nghĩa là “cùng với, và”. Ghép lại cấu trúc hàm, chúng ta có yêu cầu: Chỉ chọn những quan sát có ID khác với 45, 149, 150, 253.
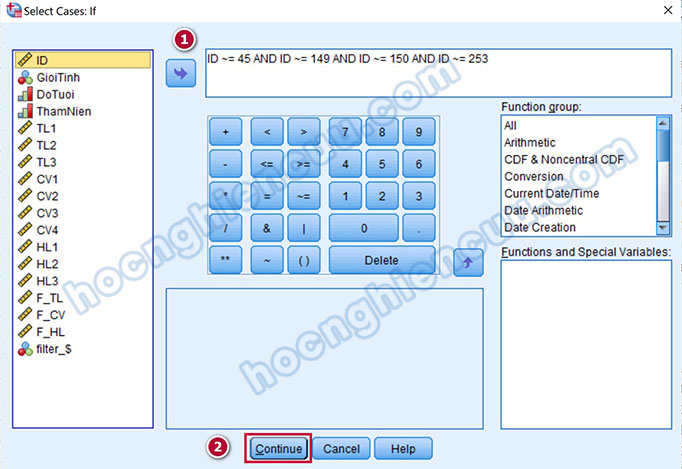
Nhấp vào Continue để trở về cửa sổ Select Cases, tiếp tục nhấp vào OK để hàm được thực hiện. Lúc này trên giao diện Data View, các quan sát 45, 149, 150, 253 đều được gạch bỏ, nghĩa là khi tính toán, phần mềm sẽ xem như không có các quan sát này trong dữ liệu. Thực hiện hồi quy tuyến tính bội với tập dữ liệu đã được loại bỏ các quan sát dị biệt để xem xét sự thay đổi.
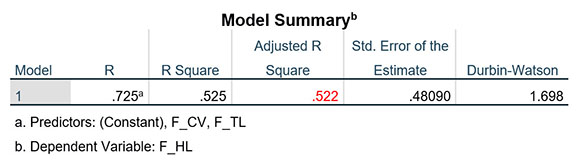
Giá trị Adjusted R Square mới trong bảng Model Summary bằng 0.522, so với giá trị ban đầu là 0.478 thì độ phù hợp mô hình tăng lên rất đáng kể. Đánh đổi sự cải thiện độ phù hợp mô hình hồi quy, chúng ta loại đi 3 quan sát dị biệt. Số lượng 3 quan sát so với cỡ mẫu 350 là rất nhỏ, do vậy, chúng ta nên loại bỏ các quan sát dị biệt này để có được kết quả hồi quy tốt hơn.
Kỹ thuật xử lý điểm dị biệt dựa vào đồ thị Boxplot không chỉ áp dụng được cho trường hợp cải thiện kết quả hồi quy tuyến tính bội, chúng ta hoàn toàn có thể linh động sử dụng ở các biến quan sát để cải thiện kết quả Cronbach’s Alpha, EFA, CFA, …
Xem tiếp: Nhận diện điểm dị biệt bằng hồi quy tuyến tính trong SPSS