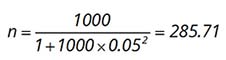1. Yếu tố ảnh hưởng tới quyết định chọn cỡ mẫu
Kích thước mẫu (cỡ mẫu) của nghiên cứu càng lớn, sai số trong các ước lượng sẽ càng thấp, khả năng đại diện cho tổng thể càng cao. Tuy nhiên, việc thu thập cỡ mẫu lớn sẽ làm tiêu tốn nhiều thời gian, công sức, tiền bạc ở toàn bộ các khâu từ thu thập, kiểm tra, phân tích. Do đó việc xác định kích thước mẫu trong nghiên cứu cần phải được xem xét một cách có cân nhắc để mọi thứ được cân bằng và hiệu quả. Sự lựa chọn cỡ mẫu sẽ phụ thuộc vào:
- Độ tin cậy cần có của dữ liệu. Nghĩa là mức độ chắc chắn rằng các đặc điểm của cỡ mẫu được chọn phải khái quát được cho đặc điểm tổng thể.
- Sai số mà nghiên cứu có thể chấp nhận được. Đó là độ chính xác chúng ta yêu cầu cho bất ký ước lượng được thực hiện trên mẫu.
- Các loại kiểm định, phân tích sẽ thực hiện. Một số kỹ thuật thống kê yêu cầu cỡ mẫu phải đạt một ngưỡng nhất định thì các ước lượng mới có ý nghĩa.
- Kích thước của tổng thể. Mẫu nghiên cứu sẽ cần chiếm một tỷ lệ nhất định so với kích thước của tổng thể.
2. Xác định cỡ mẫu theo ước lượng tổng thể
Theo Yamane Taro (1967), việc xác định kích thước mẫu sẽ được chia làm hai trường hợp: không biết tổng thể và biết được tổng thể.
2.1 Kích thước mẫu trường hợp không biết quy mô tổng thể
Chúng ta sẽ sử dụng công thức sau:
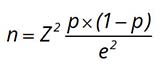
Trong đó:
- n: kích thước mẫu cần xác định.
- Z: giá trị tra bảng phân phối Z dựa vào độ tin cậy lựa chọn. Thông thường, độ tin cậy được sử dụng là 95% tương ứng với Z = 1.96.
- p: tỷ lệ ước lượng cỡ mẫu n thành công. Thường chúng ta chọn p = 0.5 để tích số p(1-p) là lớn nhất, điều này đảm bảo an toàn cho mẫu n ước lượng.
- e: sai số cho phép. Thường ba tỷ lệ sai số hay sử dụng là: ±01 (1%), ±0.05 (5%), ±0.1 (10%), trong đó mức phổ biến nhất là ±0.05.
Ví dụ: Nghiên cứu sự hài lòng của khách hàng đã dùng sản phẩm nước giải khát Pepsi tại TP.HCM. Đây là tổng thể không xác định được quy mô vì chúng ta không biết được có bao nhiêu khách hàng đã uống nước Pepsi ở TP.HCM. Như vậy cỡ mẫu tối thiểu cần có của nghiên cứu sẽ là 385 người:
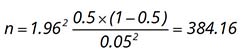
2.2 Kích thước mâu trường hợp biết quy mô tổng thể
Chúng ta sẽ sử dụng công thức tính cỡ mẫu sau:
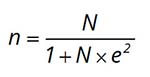
Trong đó:
- n: kích thước mẫu cần xác định.
- N: quy mô tổng thể.
- e: sai số cho phép. Thường ba tỷ lệ sai số hay sử dụng là: ±01 (1%), ±0.05 (5%), ±0.1 (10%), trong đó mức phổ biến nhất là ±0.05.
Ví dụ: Nghiên cứu sự hài lòng của khách hàng đã mua sữa bột Ensure Gold trong tháng 8 năm 2020 tại siêu thị Coopmart Phú Thọ (Quận 11, TP.HCM). Siêu thị tổng hợp danh sách khách hàng từ hệ thống thì có 1000 khách hàng, đây là tổng thể xác định được quy mô. Như vậy cỡ mẫu tối thiểu cần có của nghiên cứu nếu sai số e = ±0.05 sẽ là 286 người:
