Sử dụng tập dữ liệu thực hành có tên 350 – DLTH 1.sav của ebook SPSS 26 Phạm Lộc Blog, tương ứng với mô hình nghiên cứu và bảng câu hỏi khảo sát được giới thiệu tại bài viết Bảng khảo sát các yếu tố ảnh hưởng đến sự hài lòng của nhân viên. Sau tương quan Pearson, chúng ta có 6 biến độc lập hợp lệ để sử dụng cho phân tích hồi quy.
1. Phân tích hồi quy tuyến tính bội trên SPSS 26
Thực hiện phân tích hồi quy tuyến tính bội để đánh giá sự tác động của các biến độc lập này lên biến phụ thuộc. Chúng ta vào Analyze > Regression > Linear…
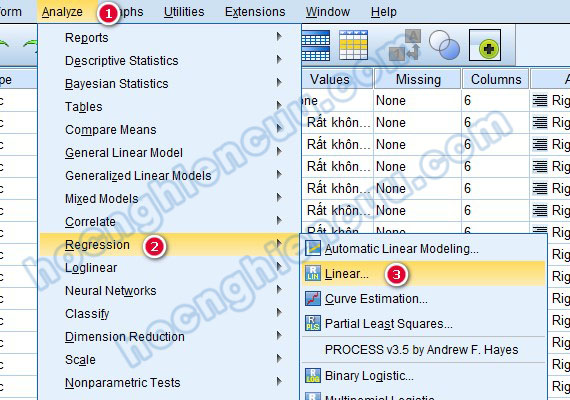
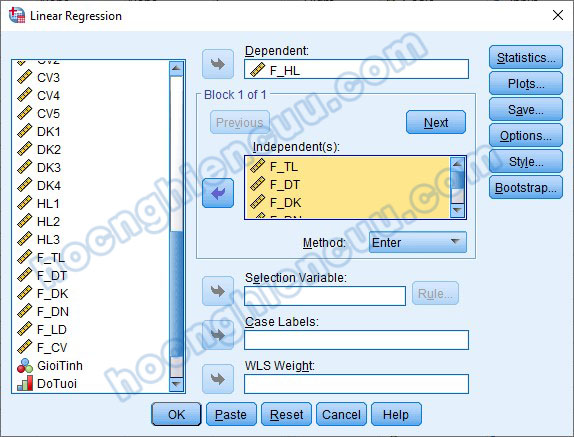
Đưa biến phụ thuộc vào ô Dependent, các biến độc lập vào ô Independents.
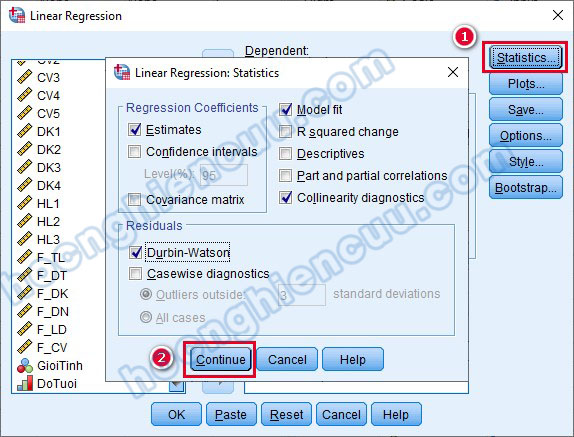
Vào mục Statistics, tích chọn các mục như trong ảnh và chọn Continue.
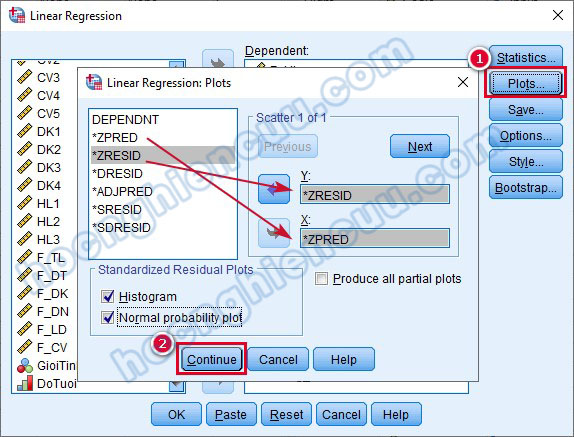
Vào mục Plots, tích chọn vào Histogram và Normal probability plot, kéo biến ZRESID thả vào ô Y, kéo biến ZPRED thả vào ô X như hình bên dưới. Tiếp tục chọn Continue.
Các mục còn lại chúng ta sẽ để mặc định. Quay lại giao diện ban đầu, mục Method là các phương pháp đưa biến vào, tùy vào dạng nghiên cứu mà chúng ta sẽ chọn Enter hoặc Stepwise. Tính chất đề tài thực hành là nghiên cứu khẳng định, do vậy tác giả sẽ chọn phương pháp Enter đưa biến vào một lượt. Tiếp tục nhấp vào OK.
SPSS sẽ xuất ra rất nhiều bảng, chúng ta sẽ tập trung vào các bảng ANOVA, Model Summary, Coefficients và ba biểu đồ Histogram, Normal P-P Plot, Scatter Plot.
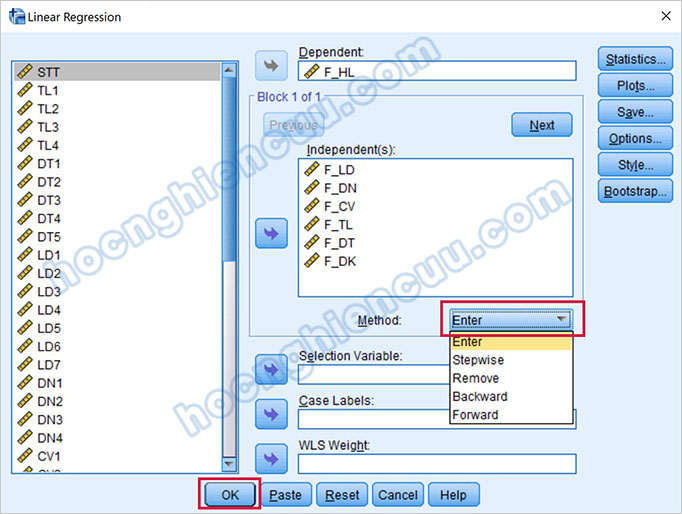
Bảng ANOVA cho chúng ta kết quả kiểm định F để đánh giá giả thuyết sự phù hợp của mô hình hồi quy. Giá trị sig kiểm định F bằng 0.000 < 0.05, do đó, mô hình hồi quy là phù hợp.

Bảng Model Summary cho chúng ta kết quả R bình phương (R Square) và R bình phương hiệu chỉnh (Adjusted R Square) để đánh giá mức độ phù hợp của mô hình. Giá trị R bình phương hiệu chỉnh bằng 0.695 cho thấy các biến độc lập đưa vào phân tích hồi quy ảnh hưởng 69.5% sự biến thiên của biến phụ thuộc, còn lại 31.4% là do các biến ngoài mô hình và sai số ngẫu nhiên.
Kết quả bảng này cũng đưa ra giá trị Durbin–Watson để đánh giá hiện tượng tự tương quan chuỗi bậc nhất. Giá trị DW = 1.849, nằm trong khoảng 1.5 đến 2.5 nên kết quả không vi phạm giả định tự tương quan chuỗi bậc nhất (Yahua Qiao, 2011).
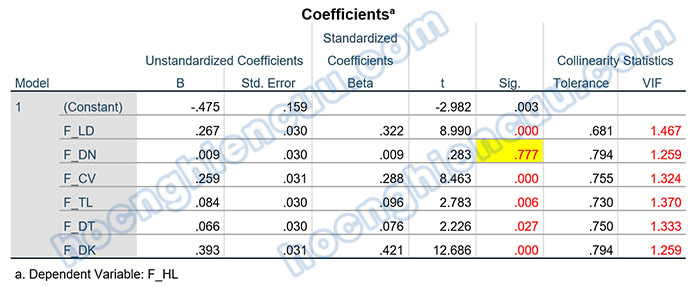
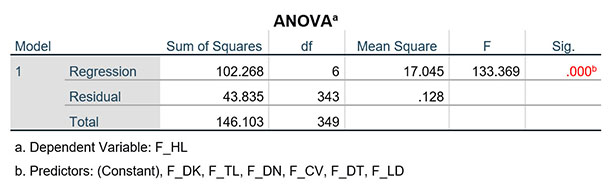
Bảng Coefficients cho chúng ta kết quả kiểm định t để đánh giá giả thuyết ý nghĩa hệ số hồi quy. Biến F_DN có giá trị sig kiểm định t bằng 0.777 > 0.05[1], do đó biến này không có ý nghĩa trong mô hình hồi quy, hay nói cách khác, biến này không có sự tác động lên biến phụ thuộc F_HL. Các biến còn lại gồm F_LD, F_CV, F_TL, F_DT, F_DK đều có sig kiểm định t nhỏ hơn 0.05, do đó các biến này đều có ý nghĩa thống kê, đều tác động lên biến phụ thuộc F_HL.
[1] Lưu ý rằng SPSS ký hiệu .031 nghĩa là 0.031. SPSS tự động loại bỏ số 0 trước dấu phẩy phần thập phân một số bảng kết quả như tương quan, hồi quy,…
2. Đánh giá giả định hồi quy tuyến tính trên SPSS 26
2.1 Giả định phân phối chuẩn của phần dư
Giả định đầu tiên đó là phần dư trong hồi quy phải xấp xỉ phân phối chuẩn. Phần dư có thể không tuân theo phân phối chuẩn vì những lý do như: sử dụng sai mô hình, phương sai không phải là hằng số, số lượng các phần dư không đủ nhiều để phân tích… Vì vậy, chúng ta cần thực hiện nhiều cách khảo sát khác nhau. Hai cách phổ biến nhất là căn cứ vào biểu đồ Histogram và Normal P-P Plot phần dư.
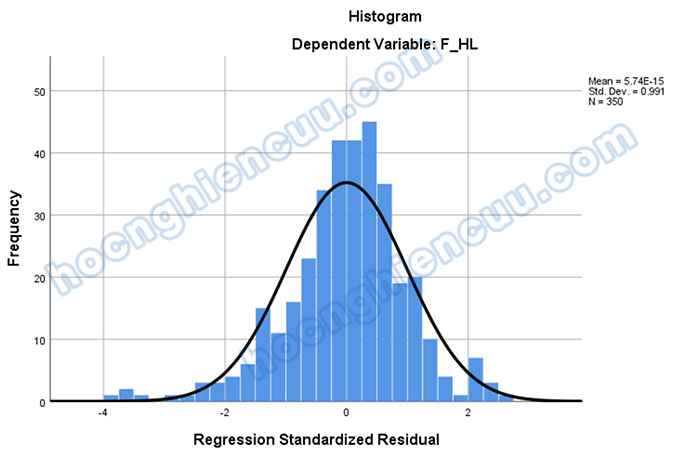
Đối với biểu đồ Histogram, nếu giá trị trung bình Mean gần bằng 0, độ lệch chuẩn Std. Dev gần bằng 1, các cột giá trị phần dư phân bố theo dạng hình chuông, ta có thể khẳng định phân phối là xấp xỉ chuẩn, giả định phân phối chuẩn của phần dư không bị vi phạm.
Đối với biểu đồ Normal P-P Plot, nếu các điểm dữ liệu trong phân phối của phần dư bám sát vào đường chéo, phần dư càng có phân phối chuẩn. Nếu các điểm dữ liệu phân bố xa đường chéo, phân phối càng “ít chuẩn”.
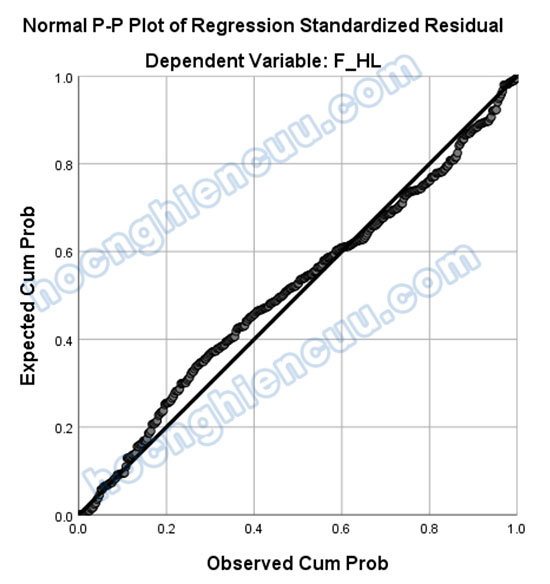
2.2 Giả định liên hệ tuyến tính giữa biến phụ thuộc với biến độc lập
Giả định thứ hai đó là phải có mối liên hệ tuyến tính giữa biến phụ thuộc với các biến độc lập. Biểu đồ phân tán Scatter Plot giữa các phần dư chuẩn hóa và giá trị dự đoán chuẩn hóa giúp chúng ta dò tìm xem dữ liệu hiện tại có vi phạm giả định liên hệ tuyến tính hay không.
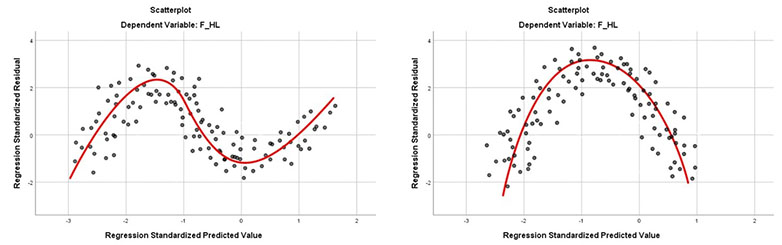
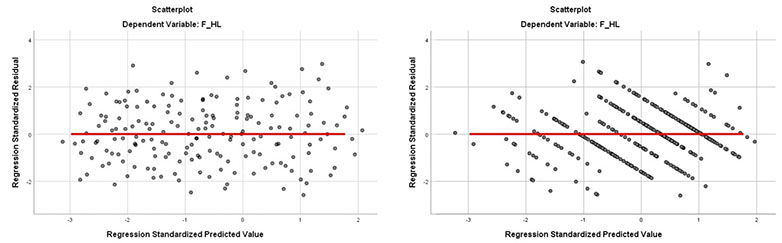
Nếu các điểm dữ liệu phân bố tập trung xung quanh đường tung độ 0 và có xu hướng tạo thành một đường thẳng, giả định liên hệ tuyến tính không bị vi phạm. Cách bố trí của điểm dữ liệu trên đồ thị scatter sẽ tùy thuộc vào bản chất biến phụ thuộc, khi đánh giá, chúng ta cần nhìn tổng quát xu hướng của đám mây điểm dữ liệu.
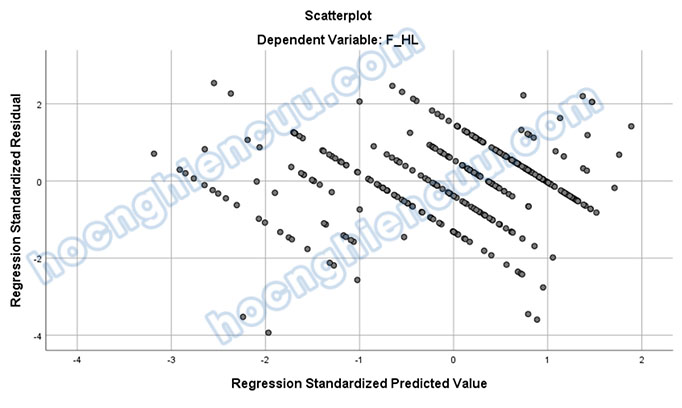
2.3 Giả định tự tương quan chuỗi bậc nhất
Phần dư của mỗi quan sát trong tập dữ liệu phải là độc lập nhau, giữa chúng không được có sự tương quan. Nếu xảy ra sự tương quan giữa các phần dư, hiện tượng tự tương quan chuỗi sẽ xuất hiện, điều này dẫn đến sự vi phạm giả định trong hồi quy.
Trị số Durbin–Watson (DW) là một đại lượng thống kê dùng để kiểm tra hiện tượng tự tương quan chuỗi bậc nhất (kiểm định tương quan của các sai số kề nhau). DW có giá trị biến thiên trong khoảng từ 0 đến 4; nếu các phần dư không có tương quan chuỗi bậc nhất với nhau thì giá trị sẽ dao động ở mức 2, nếu giá trị càng nhỏ, gần về 0 thì phần dư có tương quan thuận; nếu càng lớn, gần về 4 có nghĩa là phần dư có tương quan nghịch. Andy Field (2009)[1] cho rằng, nếu DW nhỏ hơn 1 và lớn hơn 3, chúng ta cần thực sự lưu ý bởi khả năng rất cao xảy ra hiện tượng tự tương quan chuỗi bậc nhất. Yahua Qiao (2011)[2] cho rằng, thường giá trị DW nằm trong khoảng 1.5 – 2.5 sẽ không xảy ra hiện tượng tự tương quan chuỗi bậc nhất.

[1] Andy Field, Discovering Statistics using SPSS, Sage, London, 2009.
[2] Yahua Qiao, Instertate Fiscal Disparities in America, Routledge, New York, 2011.
2.4 Giả định đa cộng tuyến
Đa cộng tuyến (multicollinearity) là hiện tượng các biến độc lập tham gia vào hồi quy có sự tương quan mạnh với nhau. Nếu hai biến độc lập tương quan mạnh với nhau, nó được gọi là hiện tượng cộng tuyến (collinearity); nếu hiện tượng cộng tuyến xảy ra giữa ba biến trở lên, nó được gọi là đa cộng tuyến. Theo Hair và cộng sự (2009), nếu xảy ra hiện tượng cộng tuyến hoặc đa cộng tuyến, các kết quả ước lượng liên quan đến biến độc lập sẽ bị sai lệch: biến có ý nghĩa trở thành không có ý nghĩa, biến tác động mạnh lại trở thành biến tác động yếu,…
Để xác định hiện tượng đa cộng tuyến, các nhà nghiên cứu thường sử dụng chỉ số VIF trong kết quả hồi quy. Hệ số phóng đại phương sai VIF) càng nhỏ càng ít khả năng xảy ra đa cộng tuyến. Hair và cộng sự (2009) cho rằng, ngưỡng VIF từ 10 trở lên sẽ xảy ra đa cộng tuyến mạnh. Nhà nghiên cứu nên cố gắng để VIF ở mức thấp nhất có thể, bởi thậm chí ở mức VIF bằng 5, bằng 3 đã có thể xảy ra đa cộng tuyến nghiêm trọng. Theo Nguyễn Đình Thọ (2010)[1], trên thực tế, nếu VIF > 2, chúng ta cần cẩn thận bởi vì đã có thể xảy ra sự đa cộng tuyến gây sai lệch các ước lượng hồi quy.

[1] Nguyễn Đình Thọ, Giáo trình phương pháp nghiên cứu khoa học trong kinh doanh, NXB Tài Chính, 2013.
