1. Lý thuyết kiểm định Chi-Square
Với việc sử dụng bảng thống kê kết hợp, chúng ta có được cái nhìn tổng quát sự liên hệ giữa hai hoặc nhiều biến định tính với nhau. Để xác định chính xác thực sự rằng có tồn tại một mối quan hệ có ý nghĩa thống kê giữa hai hay nhiều biến định tính với nhau hay không, chúng ta sẽ sử dụng tới kiểm định Chi-Square (Chi-Bình phương).
Để kiểm định Chi bình phương mối liên hệ giữa hai biến định tính, chúng ta đặt giả thuyết H0: Hai biến độc lập với nhau. Phép kiểm định Chi-Square được sử dụng để kiểm định giả thuyết này. Kết quả kiểm định:
- Sig < 0.05: Bác bỏ giả thuyết H0, nghĩa là hai biến có mối liên hệ một cách có ý nghĩa thống kê.
- Sig > 0.05: Chấp nhận giả thuyết H0, nghĩa là hai biến độc lập nhau một cách có ý nghĩa thống kê.
Trong SPSS, các số liệu của kiểm định Chi-Square được lấy từ bảng Chi-Square Tests.
Bên cạnh kiểm định Chi-Square thì SPSS 26 cũng cung cấp cho chúng ta thêm các kiểm định tương tự chức năng của Chi-Square. Nếu Chi-Square được sử dụng để đánh giá cho tất cả các dạng biến định tính, thì các kiểm định này được chia làm hai nhóm.
- Nominal: Nhóm kiểm định cho trường hợp hai biến tham gia là định danh – định danh hoặc định danh – thứ bậc.
- Ordinal: Nhóm kiểm định cho trường hợp hai biến tham gia là thứ bậc – thứ bậc.
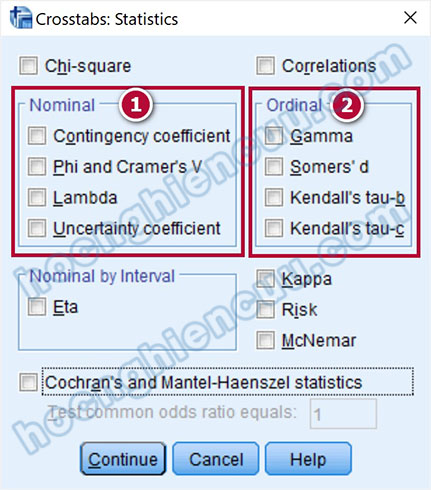
Giả thuyết chung cho tất cả các kiểm định trong hai nhóm này H0-E: Hai biến độc lập với nhau. Kết quả kiểm định:
- Sig < 0.05: Bác bỏ giả thuyết H0-E, nghĩa là hai biến có mối liên hệ một cách có ý nghĩa thống kê.
- Sig > 0.05: Chấp nhận giả thuyết H0-E, nghĩa là hai biến độc lập nhau một cách có ý nghĩa thống kê.
Trong SPSS, số liệu các kiểm định ở hai nhóm được lấy từ bảng Symmetric Measures.
2. Kiểm định Chi-Square trên SPSS 26
Sử dụng tập dữ liệu thực hành 300 – DLTH 6 – CHISQUARE.sav của ebook SPSS 26 Phạm Lộc Blog. Đây là tập dữ liệu thông tin nhân viên một công ty, chuyên viên nhân sự muốn đánh giá mối liên hệ giữa học vấn, thâm niên với mức lương để có những điều chỉnh phù hợp về chính sách lương bổng của công ty trong năm tới. Với kiểm định Chi-Square, chúng ta có thể phân tích cho từng cặp biến hoặc nhiều cặp biến cùng lúc. Trong trường hợp này, tác giả sẽ thực hiện kiểm định Chi-Square lần lượt hai biến học vấn, thâm niên với biến mức lương. Vào Analyze > Descriptives Statistics > Crosstabs…
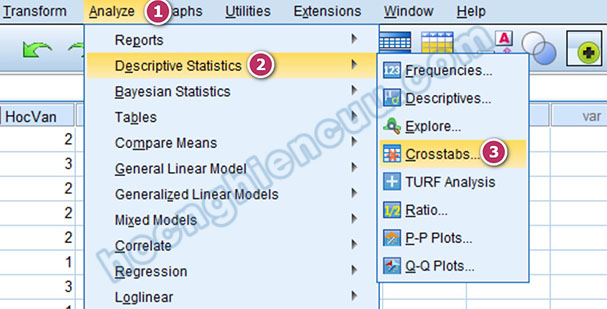
Trong cửa sổ Crosstabs, đưa biến Học vấn vào Row(s), đưa biến Mức lương vào Column(s). Chúng ta có thể đổi biến của Rows cho Columns và ngược lại, kết quả kiểm định sẽ không có sự thay đổi. Tích vào mục Display clustered bar charts để xuất biểu đồ thống kê. Trong các tùy chọn bên phải, nhấp vào Statistics…
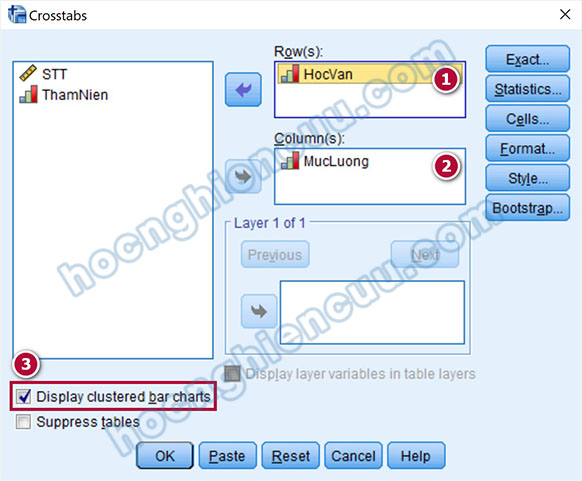
Trong tùy chọn Statistics…, tích chọn Chi-square. Học vấn là biến định danh Nominal, Mức lương là biến thứ bậc Ordinal, chúng ta sẽ sử dụng thêm một kiểm định ở mục Nominal, cụ thể ở đây tác giả chọn vào Phi and Cramer’s V. Nhấp Continue để quay lại giao diện ban đầu.
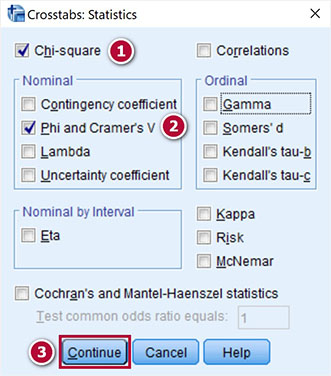
Nhấp vào tùy chọn Cells… để thiết lập một số thông số bảng kết hợp giữa hai biến tham gia kiểm định.
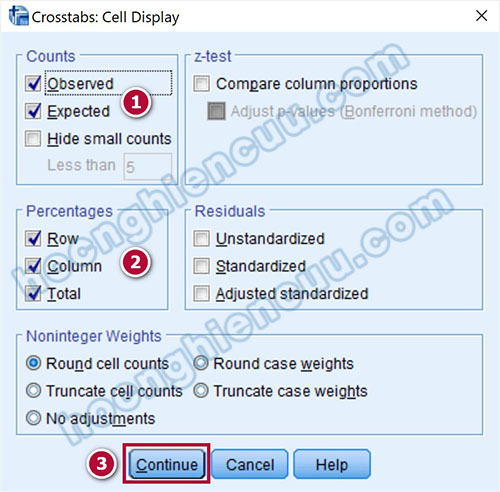
Tích chọn Observed, Expected trong mục Counts, chọn Row, Column, Total trong mục Percentages. Nhấp Continue để quay lại cửa sổ ban đầu, chọn OK để xuất kết quả ra output. Chúng ta sẽ đọc kết quả bảng Crosstabulation đầu tiên.
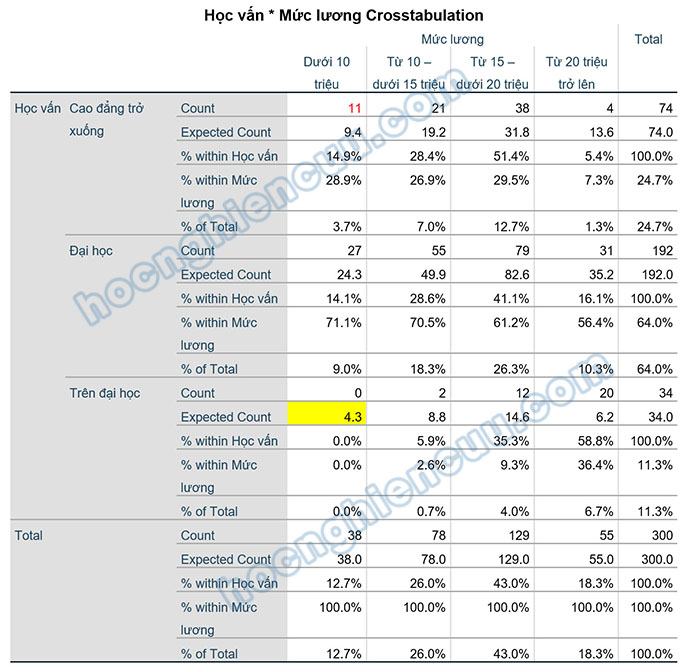
Cách đọc bảng này khá tương tự như bảng kết hợp Custom Tables trong SPSS:
- Count – Tần số quan sát: Chỉ số này cho biết số lượng đáp viên thực tế từ dữ liệu thỏa mãn điều kiện hàng và cột. Ví dụ, giá trị 11 tô đỏ ở bảng trên mang ý nghĩa là có 11 đáp viên trong tệp dữ liệu có học vấn cao đẳng trở xuống và mức lương dưới 10 triệu.
- Expected Count – Tần số kỳ vọng: Chỉ số này cho biết số lượng đáp viên mong đợi ở mỗi ô khi không có mối liên hệ giữa hai biến tham gia kiểm định. Chúng ta sẽ lưu ý giá trị này để có những điều chỉnh biến trong trường hợp số ô có tần suất mong đợi dưới 5 vượt quá tỷ lệ 20% (chi tiết hơn mời bạn xem tiếp ở bên dưới).
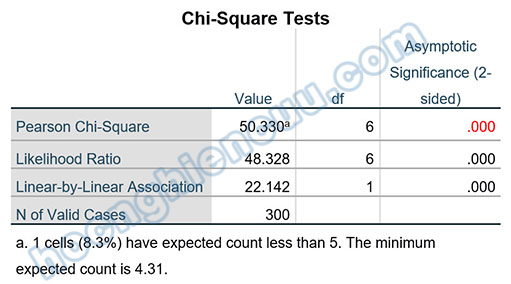
Sig kiểm định Chi-Square bằng 0.000 < 0.05, bác bỏ giả thuyết H0, nghĩa là có mối liên hệ giữa Học vấn và Mức lương.
Cuối bảng Chi-Square Tests có dòng “1 cells (8.3%) have expected count less than 5. The minimum expected count is 4.31”. Đây là dòng thông báo tỷ lệ phần trăm số ô có tần số mong đợi dưới 5, nếu con số này vượt quá 20%, kết quả kiểm định Chi-Square sẽ không còn đáng tin cậy. Cụ thể trong ví dụ thực hành, tỷ lệ này là 8.3% < 20%, do đó các chỉ số thống kê đều có tính tin cậy cao. Giả sử xảy ra tình huống số ô có tần số mong đợi dưới 5 có tỷ lệ lớn hơn 20%, chúng ta sẽ cần tìm lại các ô có Expected Count nhỏ hơn 5 trong bảng Crosstabulation để xem sự kết hợp nhóm giá trị nào giữa hai biến mà có số lượng đáp viên trả lời quá ít, từ đó dùng kỹ thuật mã hóa lại biến trong SPSS để tăng số lượng đáp viên lên. Ví dụ, trong bảng Crosstabulation bên trên, ô bôi nền vàng có tần số kỳ vọng bằng 4.3 < 5. Điều này cho biết, số đáp viên vừa có học vấn trên đại học, vừa có mức lương dưới 10 triệu chiếm số lượng rất nhỏ. Do ở đây tỷ lệ số ô như vậy chỉ chiếm tỷ lệ 8.3% < 20%, nên không có vấn đề gì nghiêm trọng với tính tin cậy của kiểm định Chi-Square. Nếu trường hợp tỷ lệ trên 20%, chúng ta cần tìm cách mã hóa lại biến Học vấn hoặc biến Mức lương để giảm tỷ lệ này xuống.
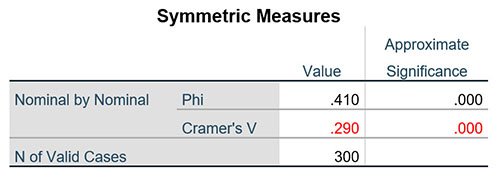
Bảng Symmetric Measures cho biết kết quả các kiểm định trong hai mục Nominal và Ordinal, trong trường hợp này là Phi và Cramer’s V. Kiểm định Phi chỉ phù hợp khi xem xét mối quan hệ giữa hai biến mà mỗi biến chỉ có hai giá trị (bảng 2×2), nếu một trong hai biến có từ ba giá trị trở lên chúng ta sẽ dùng kết quả của Cramer’s V. Cụ thể trong trường hợp này, biến Học vấn và Mức lương đều có nhiều hơn hai nhóm giá trị, chúng ta sẽ đọc kết quả ở hàng Cramer’s V. Chỉ số Approximate Significance là giá trị sig kiểm định, chỉ số Value cho biết mức độ mạnh/yếu mối liên hệ giữa hai biến. Value nằm trong đoạn [0,1], càng tiến gần về 0 mức độ liên hệ giữa hai biến càng yếu, càng tiến gần về 1 mức độ liên hệ giữa hai biến càng mạnh. Các đoạn giá trị của Value (lưu ý, chỉ đánh giá mức độ liên hệ khi giá trị sig kiểm định nhỏ hơn 0.05):
- Value ≥5: liên hệ rất mạnh
- 3 ≤ Value < 0.5: liên hệ mạnh
- 1 ≤ Value < 0.3: liên hệ trung bình
Cụ thể trong ví dụ thực hành, sig kiểm định Cramer’s V bằng 0.000 < 0.05 và Value = 0.290, như vậy Học vấn và Mức lương có mối liên hệ trung bình với nhau.
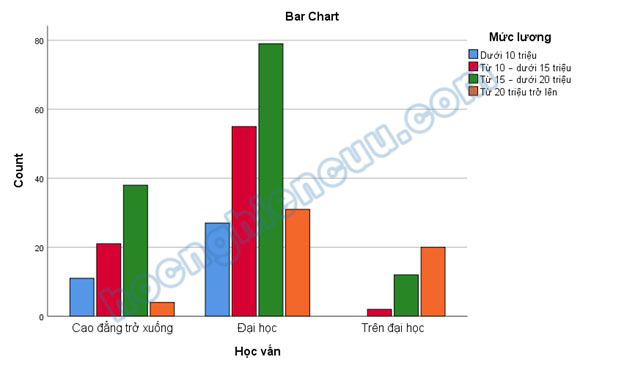
Biểu đồ Bar Chart biểu diễn mối liên hệ số lượng đáp viên giữa hai biến tham gia kiểm định. Có thể dễ dàng thấy được đáp viên có học vấn Đại học và thu nhập từ 10 đến dưới 20 triệu chiếm số lượng khá lớn trong tổng số đáp viên.
Thực hiện kiểm định Chi-Square cho trường hợp biến Thâm niên với Mức lương. Mọi thiết lập đều tương tự như biến Học vấn, chỉ có một chút thay đổi ở tùy chọn Statistics… Hai biến Thâm niên và Mức lương đều có dạng thứ bậc Ordinal, chúng ta sẽ sử dụng một kiểm định trong Ordinal, cụ thể ở đây tác giả chọn Gamma.
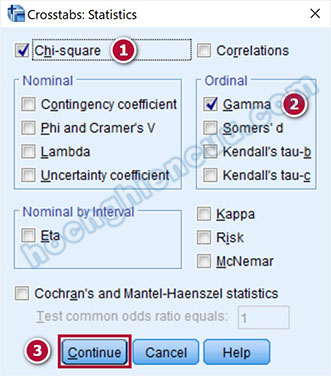
Cách đọc kết quả output sẽ giống như trường hợp biến Học vấn, riêng ở bảng Symmetric Measures chúng ta sẽ nhận xét về kiểm định Gamma.
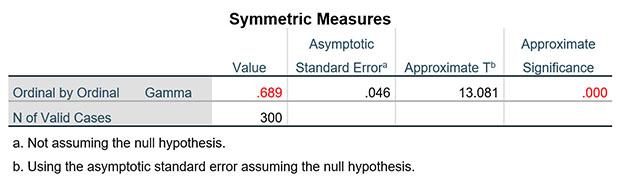
Chỉ số Approximate Significance là giá trị sig kiểm định, chỉ số Value cho biết mức độ mạnh/yếu mối liên hệ giữa hai biến. Value nằm trong đoạn [-1,1], nếu Value mang giá trị âm, hai biến có mối liên hệ nghịch, nếu Value mang giá trị dương, hai biến có mối liên hệ thuận. Khi đánh giá độ mạnh của mối liên hệ, chúng ta sẽ xem xét trị tuyệt đối của Value. Nếu trị tuyệt đối Value càng tiến gần về 1 mức độ liên hệ giữa hai biến càng mạnh, càng tiến gần về 0 mức độ liên hệ giữa hai biến càng yếu. Các đoạn giá trị khi xem xét trị tuyệt đối của Value (lưu ý, chỉ đánh giá mức độ liên hệ khi giá trị sig kiểm định nhỏ hơn 0.05):
- |Value| ≥ 5: liên hệ rất mạnh
- 3 ≤ |Value| < 0.5: liên hệ mạnh
- 1 ≤ |Value| < 0.3: liên hệ trung bình
Cụ thể trong ví dụ thực hành, sig kiểm định Gamma bằng 0.000 < 0.05 và Value = 0.689, như vậy Thâm niên và Mức lương có mối liên hệ rất mạnh với nhau.
