1. Mục đích sử dụng
Nếu như thống kê tần số mạnh về phần đưa ra số lượng các giá trị, cơ cấu phần trăm các giá trị của biến thì thống kê trung bình thiên về cung cấp các giá trị tính toán tổng quát của biến như giá trị nhỏ nhất, giá trị lớn nhất, giá trị trung bình, độ lệch chuẩn,… Do kết quả của thống kê trung bình đến từ các phép tính toán, nên các biến được đưa vào thống kê trung bình cần phải là biến định lượng.
Dựa trên kết quả thống kê trung bình, chúng ta sẽ biết được phạm vi giá trị của biến thông qua giá trị nhỏ nhất/giá trị lớn nhất. Dựa vào đây, chúng ta sẽ đánh giá khoảng giá trị đó có phù hợp với tính chất bài nghiên cứu hay không. Ví dụ, nếu câu hỏi sử dụng thước đo Likert 5 mức độ từ 1 đến 5, nhưng kết quả thống kê trung bình lại cho thấy giá trị nhỏ nhất của câu hỏi là 0 và giá trị lớn nhất là 55. Chúng ta biết được đã có vấn đề trong dữ liệu của mình và cần phải rà soát, xử lý. Giá trị trung bình Mean cho biết trung bình giá trị của biến nằm ở mức độ nào so với ngưỡng giá trị nhỏ nhất, lớn nhất. Ví dụ, câu hỏi A sử dụng thước đo Likert 5 mức độ đồng ý tăng dần từ 1 đến 5 (1 – rất không đồng ý và 5 – rất đồng ý). Kết quả thống kê cho thấy trung bình Mean của A là 1.82, mức điểm này nằm sát giá trị 2 và nhỏ hơn mức 3 trung lập, điều này cho thấy rằng đáp viên không đồng ý với ý kiến của câu hỏi đưa ra.

Thống kê mô tả như thống kê tần số hay thống kê trung bình, chức năng chính của chúng là mô tả đặc điểm dữ liệu một cách khái quát. Các chỉ số thống kê cần dùng cũng như cách đọc kết quả, diễn giải hoàn toàn tùy thuộc vào mục đích, ý đồ của người làm nghiên cứu, không có bất kỳ quy định hay quy tắc ràng buộc cứng nhắc nào về cách nhận xét.
2. Đánh giá điểm trung bình theo thước đo Likert
Likert là loại thước đo thường được sử dụng trong các nghiên cứu kinh tế để đo lường những khái niệm trừu tượng liên quan đến hành vi, thái độ. Thước đo Likert gốc biểu thị cho mức độ đồng ý tăng dần, tuy nhiên, tùy tính chất đề tài nghiên cứu thước đo này có thể được điều chỉnh cho phù hợp. Thước đo Likert có mức giá trị là một số lẻ như 3 mức độ, 5 mức độ, 7 mức độ… với một giá trị trung lập ở giữa chia đều giá trị ở hai phía. Ví dụ thước đo Likert-3 có giá trị trung lập là 2 (giữa 1 và 3), thước đo Likert-5 có giá trị trung lập là 3 (giữa 1-2 và 4-5). Phạm vi tài liệu này sẽ giới thiệu phần đánh giá điểm trung bình đối với Likert 5 mức độ đồng ý, các thước đo Likert-3, Likert-7, Likert-9… sẽ áp dụng tương tự. Dưới đây là hai phép đánh giá trung bình theo thước đo Likert được sử dụng phổ biến hiện nay. Thước đo Likert 5 mức độ gồm các giá trị:

Hướng đánh giá 1: Dựa theo quy tắc làm tròn toán học
Theo nguyên tắc toán học, nếu giá trị trung bình làm tròn tới số nguyên đầu tiên gần mức giá trị nào của thước đo Likert nhất, chúng ta sẽ đánh giá nó ở mức giá trị đó.
Chúng ta sẽ có các đoạn giá trị:
- 00 – 1.49 (làm tròn thành 1): Rất không đồng ý
- 50 – 2.49 (làm tròn thành 2): Không đồng ý
- 50 – 3.49 (làm tròn thành 3): Trung lập
- 50 – 4.49 (làm tròn thành 4): Đồng ý
- 50 – 5.00 (làm tròn thành 5): Rất đồng ý
Xét về tính ứng dụng, cách đánh giá này dễ hiểu, dễ nhớ, dễ thực hiện bởi nguyên tắc làm tròn toán học hầu như chúng ta ai cũng đều nắm rõ. Tuy nhiên, việc làm tròn khiến cho hai giá trị nhỏ nhất là 1 và lớn nhất là 5 có mức giá trị dao động nhỏ hơn so với ba giá trị còn lại. Ví dụ, từ 1.00 đến 1.49, phạm vi dao động giá trị là 0.49, trong khi đó từ 1.50 đến 2.49, mức dao động lên tới 0.99.
Hướng đánh giá 2: Dựa theo giá trị khoảng cách
Chia thước đo Likert 5 mức độ đồng ý thành 5 phần đều nhau và phân phối mỗi phần tương ứng với một giá trị của thước đo:
Giá trị khoảng cách = (Maximum – Minimum) / 5 = (5-1)/5 = 0.8
Chúng ta sẽ có các đoạn giá trị:
- 00 – 1.80 (làm tròn thành 1): Rất không đồng ý
- 81 – 2.60 (làm tròn thành 2): Không đồng ý
- 61 – 3.40 (làm tròn thành 3): Trung lập
- 41 – 4.20 (làm tròn thành 4): Đồng ý
- 21 – 5.00 (làm tròn thành 5): Rất đồng ý
Với hướng đánh giá thứ hai, dễ dàng thấy được các đoạn giá trị được chia đều nhau, tạo nên sự cân bằng giữa từng mức đánh giá. Nhưng nhược điểm lại là cách chia đoạn giá trị tương đối phức tạp, khó nhớ. Một nhược điểm khác đó là khi chúng ta đã quá quen thuộc với quy tắc làm tròn toán học sẽ gặp nhiều bối rối khi nhận xét kết quả. Ví dụ, giá trị 1.80 theo hướng đánh giá thứ hai sẽ được làm tròn thành 1, trong khi theo nguyên tắc làm tròn toán học thì nó sẽ bằng 2.
3. Thống kê trung bình trên SPSS 26
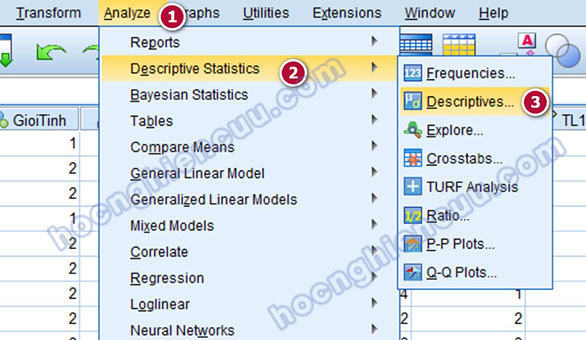
Sử dụng tập dữ liệu thực hành có tên 350 – DLTH 1.sav của ebook SPSS 26 Phạm Lộc Blog, tương ứng với mô hình nghiên cứu và bảng câu hỏi khảo sát ở chương LÝ THUYẾT ĐỀ TÀI NGHIÊN CỨU – ĐỀ TÀI THỰC HÀNH. Chúng ta sẽ thực hiện thống kê trung bình trên SPSS cho các biến thông tin cá nhân bằng cách vào Analyze > Descriptive Statistics > Descriptives…
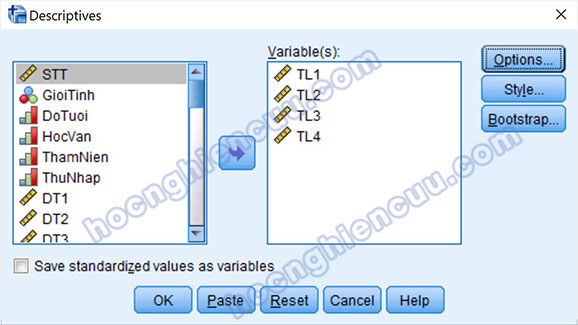
Tại cửa sổ Descriptives, đưa các biến cần thống kê trung bình vào mục Variable(s), có thể đưa cùng lúc nhiều biến vào thực hiện thống kê. Trong hướng dẫn này, tác giả sẽ thực hành mẫu với nhóm biến Tiền lương (từ TL1 đến TL4) nên tác giả sẽ đưa các biến này vào mục Variable(s).
Bên phải có các mục Options, Style và Bootstrap để chúng ta lựa chọn loại thống kê trung bình cũng như định dạng kết quả xuất ra. Tuy nhiên, thường chúng ta chỉ sử dụng đến mục Options.
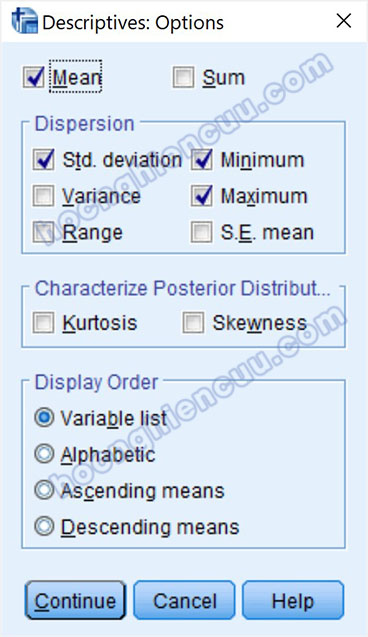
Trong Options, có các loại thống kê để chúng ta lựa chọn tùy theo mục đích đánh giá, SPSS thiết lập mặc định các mục trong phần này gồm:
- Mean: giá trị trung bình
- deviation: độ lệch chuẩn
- Minimum: giá trị nhỏ nhất
- Maximum: giá trị lớn nhất
Tác giả không tích vào thống kê nào thêm mà chỉ sử dụng mặc định SPSS đề xuất. Nhấp chuột vào Continue để quay lại cửa sổ ban đầu, nhấp vào OK để xuất kết quả ra output.
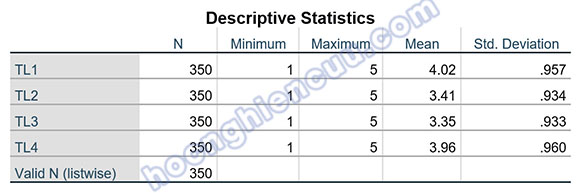
Chúng ta sẽ đọc kết quả ở bảng Descriptive Statistics. N là cột cần quan tâm trước nhất để xem có dữ liệu giá trị khuyết Missing hay không, nếu có Missing Value thì giá trị N này sẽ khác với cỡ mẫu. Tiếp tục nhìn vào kết quả giá trị nhỏ nhất, lớn nhất để xem có tình trạng giá trị vượt ngoài giới hạn thang đo hay không. Hai giá trị còn lại là trung bình và độ lệch chuẩn thường sẽ đi theo kết quả của giá trị nhỏ nhất, lớn nhất. Nếu có tình trạng giá trị vượt ngoài thang điểm đánh giá, giá trị trung bình và độ lệch chuẩn sẽ có sự đột biến.
Để đọc kết quả một cách trực quan hơn, với thống kê trung bình, chúng ta nên đưa nội dung câu hỏi vào bảng kết quả và tùy chỉnh lại bảng như bên dưới.

Đọc kết quả theo hướng đánh giá thứ nhất (làm tròn toán học), giá trị trung bình của TL2, TL3 xấp xỉ bằng 3, như vậy đáp viên có ý kiến trung lập với quan điểm “Phân phối công bằng tiền lương, thưởng và phụ cấp theo đóng góp của nhân viên” và “Chính sách tăng lương của công ty hợp lý”. Giá trị trung bình của TL1, TL4 xấp xỉ 4, như vậy đáp viên có xu hướng đồng ý với các quan điểm “Anh/Chị được trả lương tương xứng với kết quả làm việc của mình”, “Mức lương hiện tại của Anh/Chị phù hợp so với mặt bằng chung của thị trường lao động”.
Nhìn chung, kết quả này cho thấy rằng công ty đang có chính sách về Tiền lương khá tốt khi nhân viên đều cảm thấy tương đối hài lòng với mức lương họ được nhận, về chính sách tăng lương, phân phối lương giữa các nhân viên.
