Phân tích mô hình cấu trúc tuyến tính (SEM) bằng AMOS

Phân tích mô hình cấu trúc tuyến tính (Structural Equation Modeling – SEM) bằng phần mềm AMOS được sử dụng nhằm đạt được các mục tiêu sau.

– Thứ nhất, đánh giá mức độ phù hợp tổng thể của mô hình SEM thông qua các chỉ số độ phù hợp mô hình như Chi-square/df, Comparative Fit Index (CFI), Tucker–Lewis Index (TLI), Goodness of Fit Index (GFI) và Root Mean Square Error of Approximation (RMSEA).

– Thứ hai, kiểm định ý nghĩa thống kê của các mối quan hệ tác động trực tiếp cũng như các mối quan hệ trung gian giữa các biến trong mô hình nghiên cứu.

– Thứ ba, xác định chiều hướng tác động và mức độ ảnh hưởng mạnh hay yếu của các mối quan hệ giữa các biến tiềm ẩn trong mô hình SEM.

Phân tích SEM được thực hiện trên phần mềm AMOS. Trong bài viết trước về hướng dẫn phân tích CFA trên AMOS, mô hình nghiên cứu đã được xây dựng và trình bày. Trong nghiên cứu này, mô hình đó tiếp tục được kế thừa và sử dụng cho phân tích SEM nhằm kiểm định các giả thuyết nghiên cứu đề xuất.

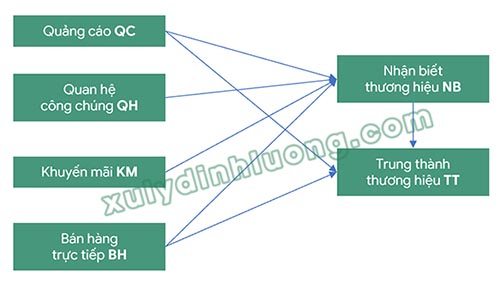
Cấu trúc các biến trong mô hình bao gồm các biến tiềm ẩn và biến quan sát như sau:

– Biến Quảng cáo (QC) được đo lường bởi 5 biến quan sát;

– Biến Quan hệ công chúng (QH) gồm 5 biến quan sát;

– Biến Khuyến mãi (KM) gồm 4 biến quan sát;

– Biến Bán hàng trực tiếp (BH) gồm 6 biến quan sát;

– Biến Nhận biết thương hiệu (NB) gồm 4 biến quan sát;

– Và biến Trung thành thương hiệu (TT) gồm 5 biến quan sát.

Tuy nhiên, trong các bước phân tích độ tin cậy Cronbach’s Alpha, phân tích nhân tố khám phá (EFA) và phân tích nhân tố khẳng định (CFA) trước đó, ba biến quan sát gồm QC4, QH1 và BH6 đã bị loại do không đạt yêu cầu về độ tin cậy và giá trị đo lường. Do đó, các biến này không tiếp tục được sử dụng trong quá trình phân tích SEM.

Trên cơ sở mô hình nghiên cứu đã đề xuất, nghiên cứu tiến hành kiểm định bảy giả thuyết cụ thể.

Giả thuyết H1 cho rằng quảng cáo có tác động đến nhận biết thương hiệu.

Giả thuyết H2 cho rằng quan hệ công chúng có tác động đến nhận biết thương hiệu.

Giả thuyết H3 đề xuất khuyến mãi có tác động đến nhận biết thương hiệu.

Giả thuyết H4 cho rằng bán hàng trực tiếp có tác động đến nhận biết thương hiệu.

Giả thuyết H5 cho rằng quảng cáo có tác động đến trung thành thương hiệu.

Giả thuyết H6 cho rằng bán hàng trực tiếp có tác động đến trung thành thương hiệu.

Cuối cùng, giả thuyết H7 cho rằng nhận biết thương hiệu có tác động đến trung thành thương hiệu.

1. Xây dựng diagram SEM từ diagram CFA

Trong trường hợp nghiên cứu đã thực hiện phân tích nhân tố khẳng định (CFA) trước khi tiến hành mô hình cấu trúc tuyến tính (SEM), nhà nghiên cứu có thể tận dụng trực tiếp diagram CFA để chuyển đổi sang SEM, qua đó tiết kiệm thời gian và đảm bảo tính nhất quán của mô hình đo lường. Tại giao diện diagram CFA trong phần mềm AMOS, thực hiện thao tác File > Save as và lưu tệp với tên mới là SEM để tạo một bản sao phục vụ cho phân tích cấu trúc.

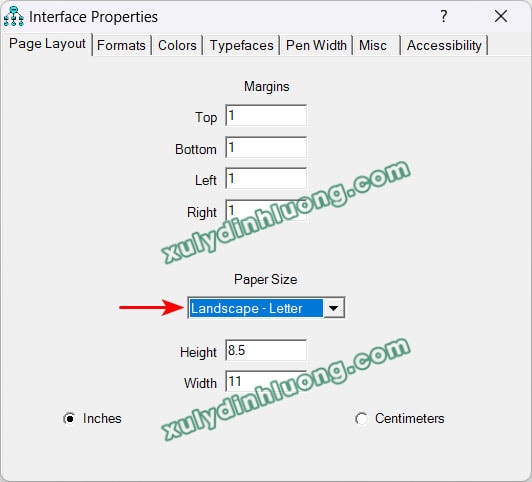
Tùy thuộc vào đặc điểm trình bày của mô hình nghiên cứu, có thể giữ nguyên khổ giấy mặc định nếu mô hình phù hợp với khổ giấy dọc. Trường hợp mô hình được trình bày rõ ràng hơn trên khổ giấy ngang, cần thực hiện thay đổi bố cục trang trước khi chỉnh sửa. Từ cửa sổ AMOS, chọn View > Interface Properties.

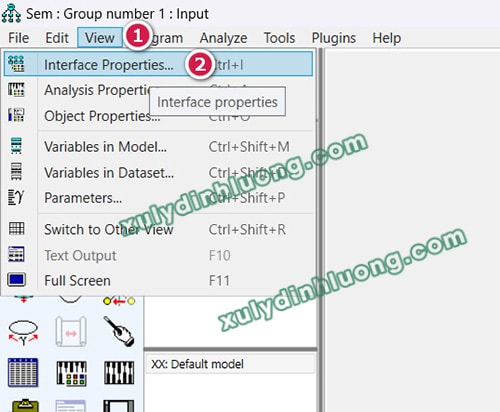
Trong cửa sổ thiết lập, tại thẻ Page Layout, ở mục Paper Size, lựa chọn Landscape – Letter, sau đó đóng cửa sổ bằng cách nhấp vào biểu tượng X ở góc trên bên phải để xác nhận và áp dụng thay đổi.

Tiếp theo, sử dụng công cụ xóa đối tượng của AMOS để loại bỏ toàn bộ các mũi tên hai chiều biểu diễn quan hệ hiệp phương sai (covariance) giữa các biến tiềm ẩn trong mô hình CFA. Bước này nhằm chuẩn bị cho việc tái cấu trúc mô hình theo định hướng SEM. Trong trường hợp chưa quen với các công cụ thao tác trong AMOS, người nghiên cứu có thể tham khảo các tài liệu hoặc video hướng dẫn Cách sử dụng AMOS để vẽ diagram CFA, SEM .

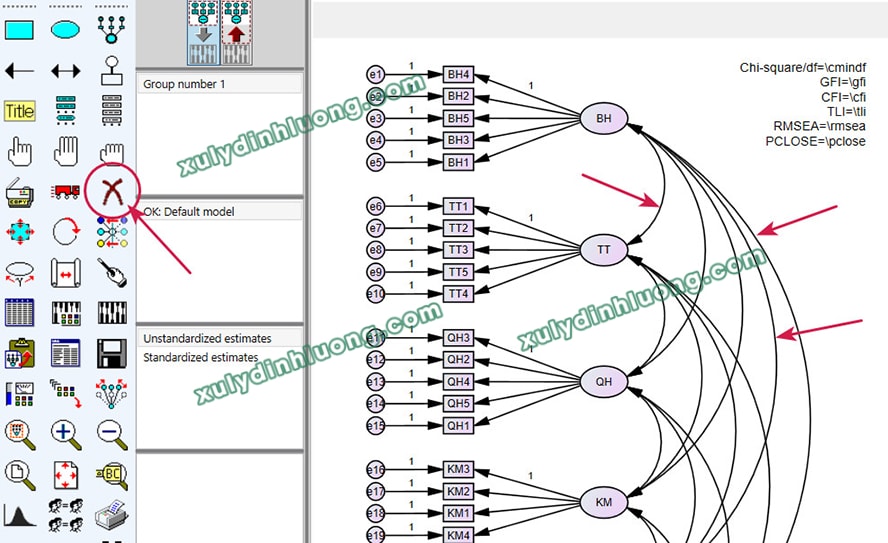
Sau khi đã xóa các mối liên hệ hiệp phương sai, sử dụng các công cụ di chuyển, căn chỉnh và xoay để sắp xếp lại vị trí các biến tiềm ẩn sao cho phù hợp với cấu trúc của mô hình lý thuyết đề xuất. Đồng thời, có thể sử dụng công cụ Title để chèn các chỉ số đánh giá mức độ phù hợp của mô hình (model fit indices) trực tiếp lên diagram. Khi bố trí sơ đồ, nên để trống một khoảng không gian ở phía bên phải các biến độc lập nhằm thuận tiện cho việc vẽ các mũi tên hiệp phương sai sau này.

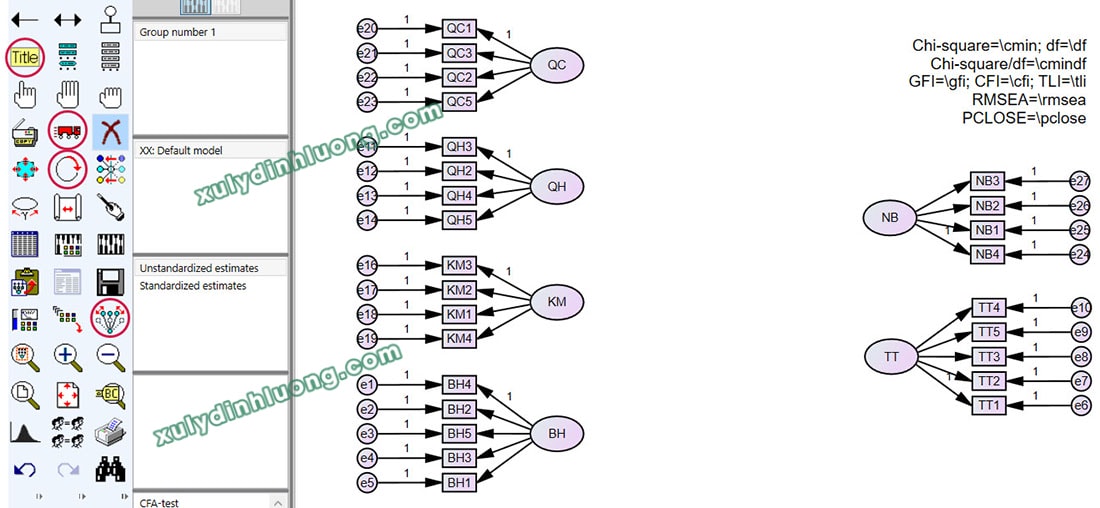
Tiếp theo, vẽ các mũi tên hai chiều để nối các biến tiềm ẩn có vai trò là biến độc lập. Trong mô hình nghiên cứu, biến độc lập được hiểu là những biến chỉ có mũi tên tác động hướng ra các biến khác và không nhận mũi tên tác động hướng vào.

Việc thiết lập mũi tên hiệp phương sai giữa các biến độc lập có ý nghĩa khai báo với phần mềm AMOS rằng các biến này có thể tương quan với nhau trong quá trình ước lượng mô hình SEM. Nếu không vẽ các mũi tên hai chiều này, AMOS sẽ chỉ phân tích các mối quan hệ nhân quả được chỉ định mà không xem xét khả năng tồn tại tương quan giữa các biến độc lập. Cách tiếp cận này thường không phù hợp trong nghiên cứu thực nghiệm, bởi các biến độc lập khi cùng tác động lên một biến phụ thuộc thường có mối liên hệ nhất định với nhau, chứ không tồn tại một cách hoàn toàn độc lập. Đồng thời, việc không xét đến tương quan giữa các biến độc lập cũng có thể bỏ qua vấn đề cộng tuyến, vốn ảnh hưởng đến độ chính xác của các ước lượng trong mô hình.

Khi vẽ mũi tên hiệp phương sai, có thể thử nối theo chiều từ biến phía trên xuống biến phía dưới hoặc ngược lại để quan sát hướng cong của đường hiệp phương sai. Nên lựa chọn cách vẽ sao cho phần lồi của đường cong nằm trong khoảng không gian trống, tránh chồng chéo lên các thành phần khác của sơ đồ.

Sau khi hoàn tất việc nối các mũi tên hai chiều, tiếp tục sử dụng các công cụ căn chỉnh và tối ưu hiển thị, nhấp lần lượt vào các biến tiềm ẩn để đảm bảo sơ đồ có bố cục rõ ràng và dễ quan sát.

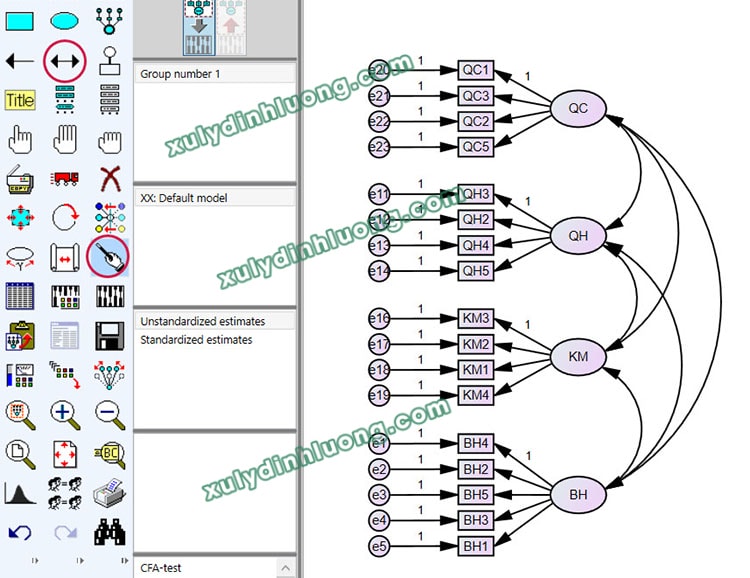
Dựa trên mô hình nghiên cứu đề xuất, tiến hành vẽ các mũi tên một chiều biểu diễn mối quan hệ tác động giữa các biến tiềm ẩn. Sau mỗi thao tác vẽ, nên tiếp tục sử dụng công cụ làm đẹp để điều chỉnh vị trí và hình dạng các đối tượng, nhằm đảm bảo tính trực quan và khoa học của diagram SEM.

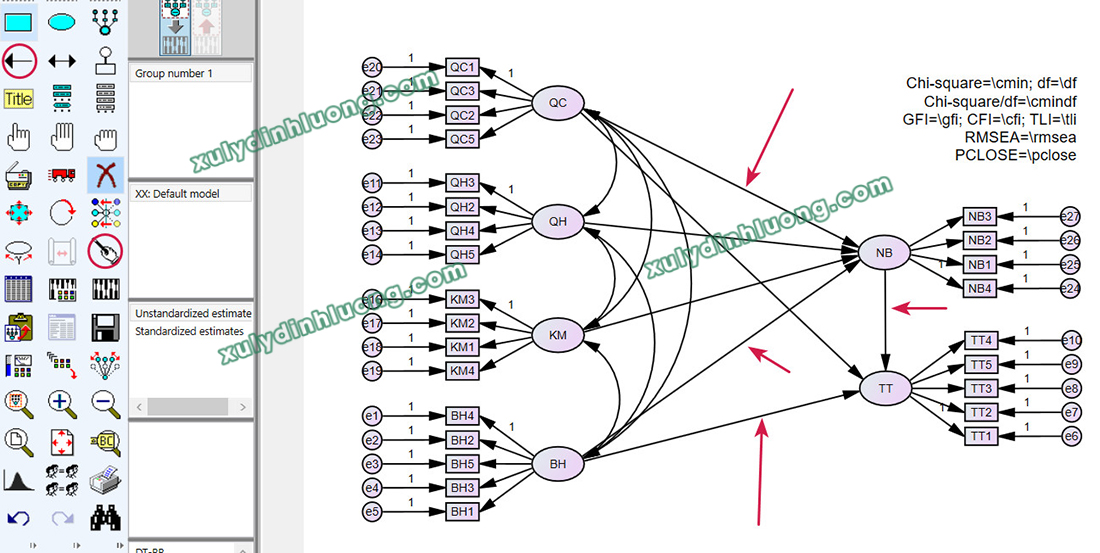
Trong mô hình, hai biến NB và TT là các biến nhận mũi tên tác động từ biến khác, do đó được xác định là biến phụ thuộc. Vì vậy, cần biểu diễn phần dư hoặc sai số cho hai biến này. Chọn biểu tượng phần dư/sai số và nhấp chuột vào biến NB. Lần nhấp đầu tiên sẽ tạo phần dư với hướng xoay mặc định; nếu hướng này chưa phù hợp, tiếp tục nhấp chuột vào biến cho đến khi phần dư có vị trí mong muốn. Thực hiện thao tác tương tự đối với biến TT.

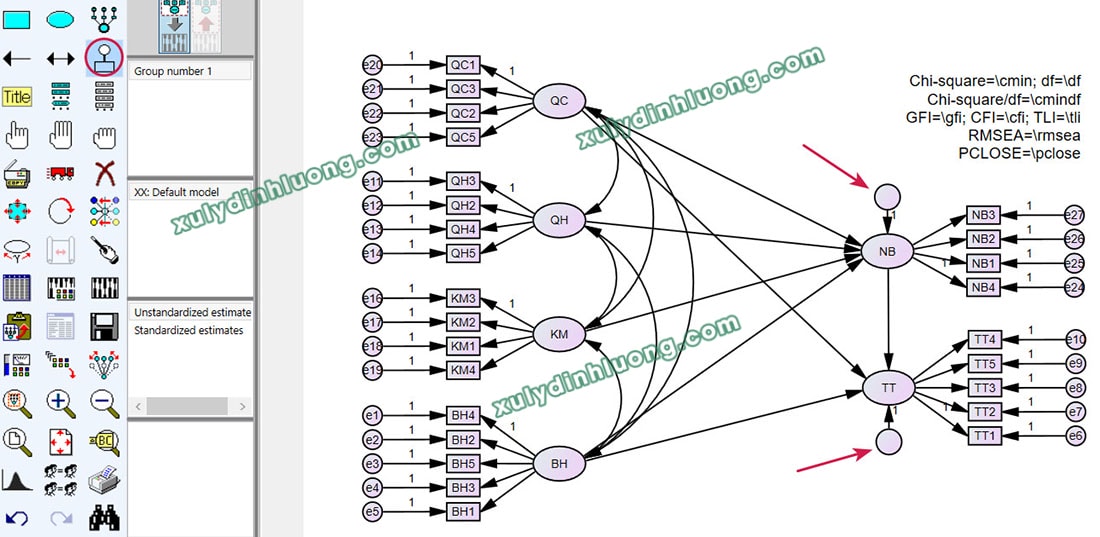
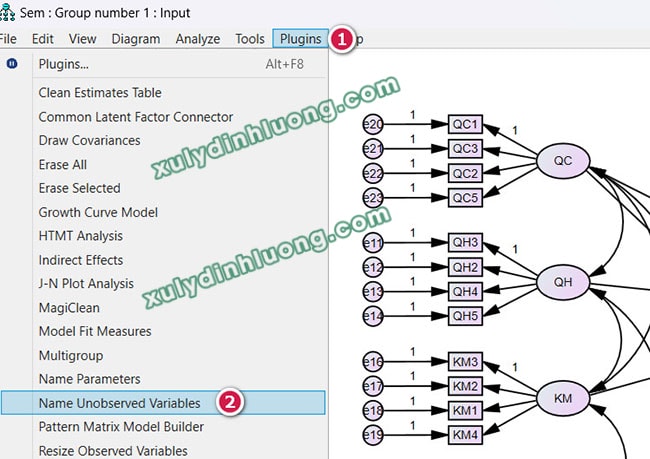
Tại thời điểm này, các phần dư gán cho hai biến NB và TT chưa được đặt tên. Nhà nghiên cứu cần khai báo tên cho các phần dư này bằng cách nhấp đúp chuột vào từng phần dư và nhập tên tương ứng, hoặc sử dụng công cụ plugin để đặt tên hàng loạt thông qua đường dẫn Plugins > Name Unobserved Variables.

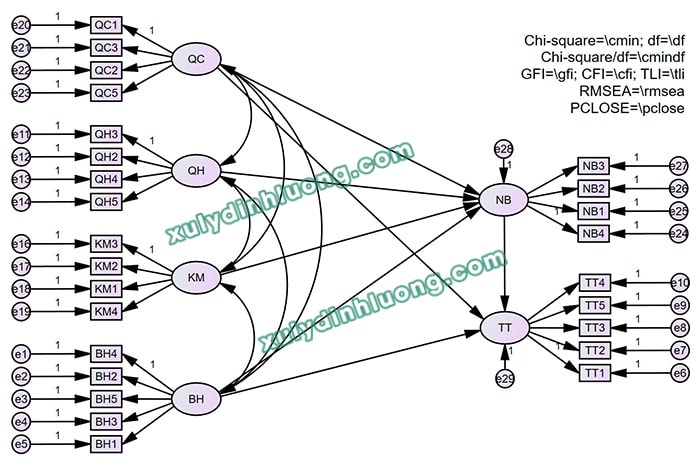
Sau khi hoàn tất các bước trên, quá trình vẽ diagram kết thúc và mô hình SEM được xây dựng đầy đủ, sẵn sàng cho bước ước lượng và phân tích kết quả.

2. Phân tích SEM trên AMOS

Bước 1: Khai báo dữ liệu SPSS cho phần mềm AMOS

Đầu tiên, người nghiên cứu nhấp chuột vào biểu tượng Select Data File trên giao diện AMOS như minh họa bên dưới.

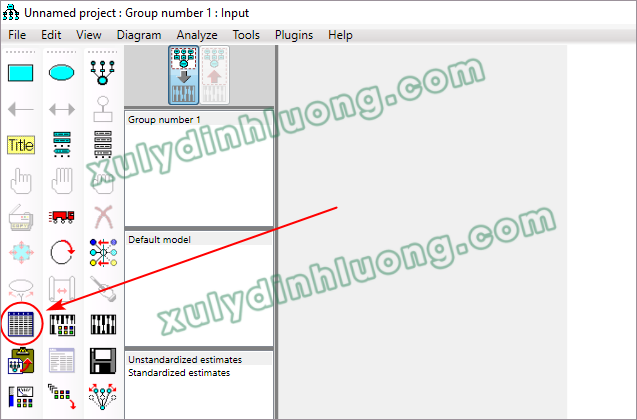
Trong hộp thoại xuất hiện, chọn mục File Name, sau đó xác định và lựa chọn tệp dữ liệu đầu vào được lưu dưới định dạng SPSS (.sav).

Trong ví dụ minh họa, tệp dữ liệu có tên DATA AMOS.sav. Sau khi lựa chọn xong tệp dữ liệu, nhấp vào nút Open để hoàn tất thao tác chọn file.

Tiếp theo, nhấp vào nút OK để phần mềm AMOS ghi nhận và liên kết với bộ dữ liệu SPSS đã được khai báo.

Bước 2: Thiết lập phân tích SEM

Từ giao diện chính của AMOS, chọn biểu tượng Analysis Properties nhằm tiến hành cấu hình các tham số phục vụ cho phân tích mô hình cấu trúc tuyến tính (SEM).

Tại cửa sổ Analysis Properties, chuyển sang thẻ Output và đánh dấu chọn các tùy chọn như minh họa trong hình. Một số thiết lập quan trọng cần lưu ý bao gồm:

• Standardized estimates: cung cấp các hệ số ước lượng chuẩn hóa, cho phép so sánh mức độ ảnh hưởng tương đối giữa các biến trong mô hình.

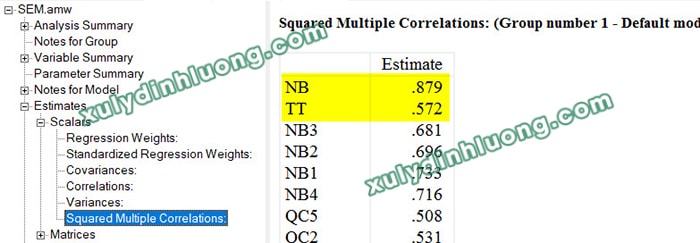
• Squared multiple correlations: hiển thị hệ số xác định R bình phương, phản ánh mức độ giải thích của các biến độc lập đối với biến phụ thuộc.

• Residual moments: cung cấp thông tin về phần dư, hỗ trợ đánh giá mức độ sai lệch giữa ma trận hiệp phương sai quan sát và ma trận ước lượng.

• Modification indices: hiển thị các chỉ số MI nhằm phát hiện những mối quan hệ tiềm năng chưa được đưa vào mô hình, từ đó xác định các nguyên nhân làm giảm mức độ phù hợp của mô hình. Việc sử dụng và diễn giải chỉ số này được trình bày chi tiết trong bài viết về Chỉ số MI – Modification Indices trong AMOS.

Sau khi hoàn tất việc lựa chọn các tùy chọn cần thiết, nhấp vào nút X ở góc trên bên phải cửa sổ để xác nhận thiết lập và thoát khỏi giao diện Analysis Properties.

Bước 3: Thực hiện phân tích mô hình cấu trúc tuyến tính (SEM)

Trong AMOS, người nghiên cứu lựa chọn biểu tượng Calculate Estimates để tiến hành ước lượng và chạy mô hình SEM.

Bên cạnh các chỉ số cơ bản được hiển thị trực tiếp trên sơ đồ mô hình, người nghiên cứu có thể nhấp chọn View Text nhằm xem toàn bộ kết quả chi tiết của phân tích SEM.

2. Đọc và diễn giải kết quả phân tích SEM trong AMOS

Kết quả phân tích SEM được xem xét thông qua ba nhóm kết quả chính, bao gồm: bảng hệ số hồi quy chưa chuẩn hóa Regression Weights, bảng hệ số hồi quy chuẩn hóa Standardized Regression Weights và bảng hệ số xác định Squared Multiple Correlations.

3.1 Bảng hệ số hồi quy chưa chuẩn hóa Regression Weights

Bảng Regression Weights cung cấp các thông tin thống kê quan trọng với các cột giá trị sau:

Estimate: Hệ số hồi quy chưa chuẩn hóa, phản ánh mức độ và chiều hướng tác động giữa các biến. Hệ số mang giá trị dương thể hiện mối quan hệ tác động cùng chiều, trong khi hệ số âm cho thấy tác động ngược chiều. Giá trị của hệ số này có thể thay đổi tùy thuộc vào cách khai báo tham số cố định cho các mũi tên liên kết giữa các biến quan sát trong cùng một nhân tố.

C.R (Critical Ratio): Giá trị kiểm định t dùng để đánh giá ý nghĩa thống kê của hệ số hồi quy. Tuy nhiên, việc đối chiếu giá trị này với bảng phân phối chuẩn là không thuận tiện, do đó trong thực tiễn nghiên cứu thường sử dụng trực tiếp giá trị p-value.

P: Giá trị p-value (mức ý nghĩa) dùng để kiểm định ý nghĩa thống kê của hệ số hồi quy. Với mức độ tin cậy 95%, tương ứng mức ý nghĩa 5% (0.05), nếu P < 0.05 thì hệ số hồi quy có ý nghĩa thống kê, ngược lại nếu P > 0.05 thì hệ số hồi quy không có ý nghĩa thống kê.

Xét kết quả thực nghiệm của mô hình nghiên cứu, bảng Regression Weights thu được như sau:

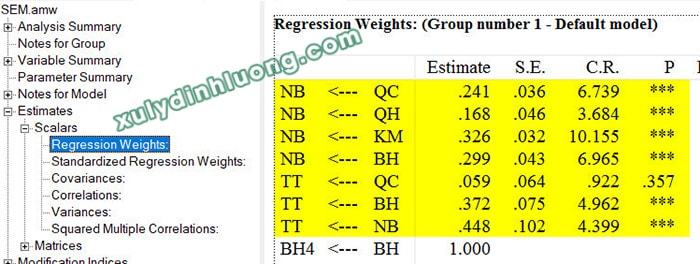
Bảng này thể hiện toàn bộ các mối quan hệ tác động giữa các biến tiềm ẩn, đồng thời bao gồm cả mối quan hệ giữa biến tiềm ẩn và các biến quan sát tương ứng. Do đó, khi diễn giải kết quả, người nghiên cứu chỉ tập trung xem xét các mối quan hệ giữa các biến tiềm ẩn trong mô hình, còn các mối quan hệ với biến quan sát có thể không cần phân tích.

→ Kết quả cho thấy, ngoại trừ mối quan hệ TT ← QC không có ý nghĩa thống kê do p-value = 0.357 lớn hơn 0.05, tất cả các mối quan hệ tác động còn lại đều có ý nghĩa thống kê vì p-value đều nhỏ hơn 0.05. Trong AMOS, ký hiệu *** được sử dụng để biểu thị giá trị p-value bằng 0.000.

→ Bên cạnh đó, các hệ số hồi quy của các mối quan hệ đều mang giá trị dương, cho thấy các tác động trong mô hình đều là tác động cùng chiều.

Cần lưu ý rằng, trong phân tích SEM, các biến hoặc mối quan hệ không có ý nghĩa thống kê không nhất thiết phải loại bỏ và chạy lại mô hình. Vấn đề này đã được giải thích chi tiết trong các nghiên cứu liên quan đến xử lý biến không có ý nghĩa trong hồi quy và SEM Biến không có ý nghĩa ở hồi quy, SEM có cần loại chạy lại không?.

Trở lại với hệ thống giả thuyết nghiên cứu được đề xuất ban đầu, mô hình bao gồm bảy giả thuyết:

H1: Quảng cáo có tác động đến Nhận biết thương hiệu

H2: Quan hệ công chúng có tác động đến Nhận biết thương hiệu

H3: Khuyến mãi có tác động đến Nhận biết thương hiệu

H4: Bán hàng trực tiếp có tác động đến Nhận biết thương hiệu

H5: Quảng cáo có tác động đến Trung thành thương hiệu

H6: Bán hàng trực tiếp có tác động đến Trung thành thương hiệu

H7: Nhận biết thương hiệu có tác động đến Trung thành thương hiệu

Việc kiểm định các giả thuyết tác động trực tiếp được thực hiện dựa trên kết quả của bảng Regression Weights. Kết quả phân tích cho thấy giả thuyết H5 bị bác bỏ, trong khi sáu giả thuyết còn lại được chấp nhận.

3.2 Bảng hệ số tác động chuẩn hóa Standardized Regression Weights

Bảng này chỉ cung cấp một cột giá trị duy nhất là Estimate, thể hiện hệ số tác động (hệ số hồi quy) đã được chuẩn hóa. Hệ số mang dấu dương phản ánh mối quan hệ tác động cùng chiều giữa các biến, trong khi hệ số mang dấu âm cho thấy mối quan hệ tác động ngược chiều.

Ý nghĩa của hệ số chuẩn hóa nằm ở khả năng cho phép so sánh mức độ ảnh hưởng mạnh hay yếu của các biến độc lập khi cùng tác động lên một biến phụ thuộc. Biến độc lập nào có giá trị tuyệt đối của hệ số chuẩn hóa lớn hơn thì được xem là có mức độ tác động mạnh hơn đến biến phụ thuộc. Cần lưu ý rằng việc so sánh này chỉ có ý nghĩa khi các biến độc lập cùng tác động lên một biến phụ thuộc duy nhất.

Dựa trên kết quả thực nghiệm của mô hình nghiên cứu đã trình bày ở trên, bảng Standardized Regression Weights cho thấy:

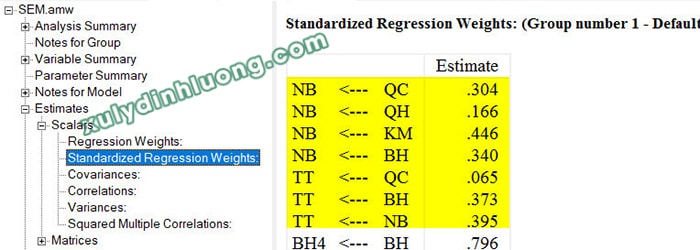
→ Mức độ tác động của các biến độc lập lên NB theo thứ tự giảm dần là: KM, tiếp đến là BH, sau đó là QC và cuối cùng là QH. Khi so sánh, sử dụng giá trị tuyệt đối của hệ số chuẩn hóa, không xét đến dấu dương hay âm của hệ số.

→ Đối với biến phụ thuộc TT, thứ tự tác động từ mạnh đến yếu của các biến độc lập là: NB, sau đó là BH. Biến QC đã được xác định là không có tác động đến TT ở phần phân tích trước, do đó không được đưa vào quá trình so sánh.

Trong trường hợp chỉ tồn tại một biến độc lập tác động đến biến phụ thuộc, việc so sánh mức độ ảnh hưởng giữa các biến là không cần thiết.