Ở bài viết Biến giả dummy và cách tạo biến giả trong SPSS, chúng ta đã tìm hiểu về khái niệm cũng như cách tạo biến giả dummy variable trên SPSS. Sau khi hoàn thành tạo biến, chúng ta sẽ sử dụng chúng như những biến độc lập bình thường để tiến hành phân tích hồi quy tuyến tính bội.
1. Ôn lại về lý thuyết về biến giả
Không phải các biến độc lập luôn ở dạng định lượng mà sẽ có các trường hợp biến độc lập là biến phân loại như học vấn (gồm trung cấp, cao đẳng, đại học, sau đại học), hôn nhân (gồm độc thân, đã lập gia đình), phòng ban (marketing, hành chính nhân sự, kế toán, kinh doanh)… Chúng ta không thực hiện hồi quy với các biến độc lập phân loại như bình thường vì các kết quả ước lượng được sẽ không có ý nghĩa. Một giải pháp để giải quyết khó khăn này đó là mã hóa biến phân loại thành biến giả (dummy variable).
Biến giả chỉ gồm hai giá trị 0 và 1. Biến giả có thể là một biến hoặc nhiều biến tùy thuộc vào đặc điểm của biến phân loại cần chuyển đổi. Ví dụ, biến phân loại giới tính gồm hai giá trị nam – nữ, chúng ta chỉ cần dùng một biến giả X1:
- X1 = 0: nam
- X1 = 1: nữ
Nếu biến phân loại chỉ có hai giá trị thì chúng ta hoàn toàn có thể mã hóa ngược lại, nam sẽ mang giá trị 1 và nữ mang giá trị 2, không có sự khác biệt.
Trường hợp biến phân loại có từ ba giá trị trở lên, chúng ta sẽ cần nhiều hơn một biến giả. Số biến giả cần tạo sẽ bằng số giá trị của biến phân loại trừ đi 1. Xét ví dụ biến phân loại là phòng ban một công ty gồm ba giá trị: phòng marketing, phòng hành chính nhân sự, phòng kinh doanh. Lúc này số biến giả cần tạo là hai biến:
- X1 = 1 nếu là phòng marketing, X1 = 0 nếu ngược lại
- X2 = 1 nếu là phòng hành chính nhân sự, X2 = 0 nếu ngược lại
Nếu một đáp viên đồng thời không thuộc phòng marketing (X1 = 0) và phòng hành chính nhân sự (X2 = 0) thì người đó sẽ thuộc phòng còn lại là kinh doanh. Chính vì vậy mà chúng ta không cần phải có biến X3 cho giá trị thứ ba – phòng kinh doanh.
- (X1 = 1 và X2 = 0): phòng marketing
- (X1 = 0 và X2 = 1): phòng hành chính nhân sự
- (X1 = 0 và X2 = 0): phòng kinh doanh
Về mặt logic, chúng ta không thực sự cần đến biến X3 cho trường hợp thứ ba, có cũng được không có cũng không sao. Nhưng về mặt thống kê, nếu xuất hiện biến X3 sẽ gây ra hiện tượng đa cộng tuyến hoàn hảo, điều này làm sai lệch toàn bộ các ước lượng hồi quy. Trong hồi quy tuyến tính bội trên SPSS, nếu xuất hiện đa cộng tuyến hoàn hảo, biến độc lập đó sẽ được loại bỏ ra khỏi kết quả hồi quy dù chúng ta sử dụng phương pháp đưa biến nào.
2. Phân tích hồi quy tuyến tính bội với biến giả trên SPSS 26
Phần thực hành này sẽ sử dụng lại biến giả đã được tạo ở bài viết Biến giả dummy và cách tạo biến giả trong SPSS, vui lòng xem lại bài viết trước để hiểu được đầy đủ phần hướng dẫn bên dưới.
Thực hiện phân tích hồi quy tuyến tính bội với các biến độc lập: TienLuong, ThamNien, BoPhan_1, BoPhan_2. Chúng ta sẽ không đưa biến BoPhan vào phân tích hồi quy mà thay vào đó sử dụng hai biến giả đã được tạo. Các giả thuyết đặt ra:
- Giả thuyết H1: Tiền lương có sự tác động đến sự hài lòng của nhân viên
- Giả thuyết H2: Thâm niên có sự tác động đến sự hài lòng của nhân viên
- Giả thuyết H3: Bộ phận có sự tác động đến sự hài lòng của nhân viên
Các bước thực hiện trên phần mềm và đọc kết quả hoàn toàn tương tự như phân tích hồi quy tuyến tính bội thông thường. Điểm khác biệt đến từ phần diễn giải ý nghĩa của các biến giả trong bảng Coefficients.
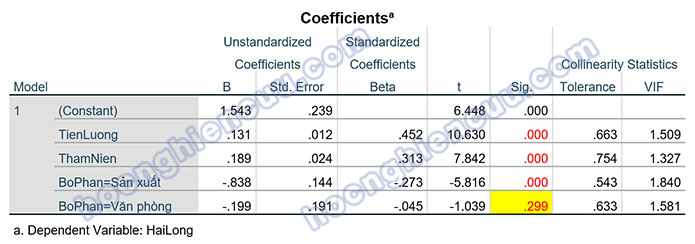
Chỉ cần một trong các biến giả có sig kiểm định t nhỏ hơn 0.05, chúng ta sẽ kết luận biến phân loại có sự tác động lên biến phụ thuộc. Cụ thể trong trường này, biến BoPhan=Sản xuất có sig kiểm định t bằng 0.000 nhỏ hơn 0.05, do đó biến BoPhan có sự tác động lên HaiLong. Vậy biến HaiLong sẽ thay đổi thế nào nếu biến BoPhan nhận các giá trị khác nhau? Trong hồi quy với biến giả, chúng ta sẽ có một nhóm giá trị làm tham chiếu, các nhóm còn lại sẽ so sánh kết quả với nhóm tham chiếu này. Bằng việc sử dụng hai biến giả cho hai giá trị đầu của biến BoPhan, chúng ta đã ngầm chọn nhóm 3 – Kinh doanh làm giá trị tham chiếu.
- 1 = Sản xuất (nhóm so sánh)
- 2 = Văn phòng (nhóm so sánh)
- 3 = Kinh doanh (nhóm tham chiếu)
Nếu sig kiểm định t của nhóm giá trị so sánh nhỏ hơn 0.05, nghĩa là sự hài lòng khác nhau giữa nhóm so sánh với nhóm tham chiếu. Ngược lại, nếu sig lớn hơn 0.05, sự hài lòng không khác nhau giữa nhóm so sánh với nhóm tham chiếu. Nếu hệ số hồi quy dương, nghĩa là sự hài lòng của nhóm so sánh cao hơn nhóm tham chiếu. Ngược lại, nếu hệ số hồi quy âm, sự hài lòng nhóm tham chiếu thấp hơn nhóm so sánh.
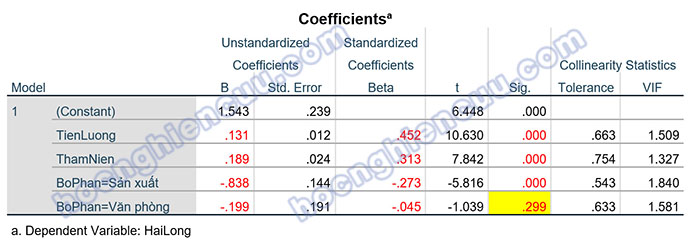
Cụ thể trong trường hợp này:
- Sig kiểm định t biến BoPhan=Sản xuất bằng 0.000 < 0.05, do đó, có khác biệt sự hài lòng giữa bộ phận Sản xuất và bộ phận Kinh doanh. Hệ số hồi quy âm nói lên rằng, bộ phận Sản xuất có sự hài lòng thấp hơn bộ phận Kinh doanh.
- Sig kiểm định t biến BoPhan=Văn phòng bằng 0.299 > 0.05, do đó, không có khác biệt sự hài lòng giữa bộ phận Văn phòng và bộ phận Kinh doanh. Khi biến không có ý nghĩa trong mô hình hồi quy, chúng ta không cần đề cập đến hệ số hồi quy.
Đến đây, chúng ta đã có thể kết luận các giả thuyết đặt ra ban đầu.

