Nội dung bài viết này chúng tôi tập trung giới thiệu tiêu chí Fornell–Larcker – một phương pháp truyền thống để kiểm định tính phân biệt của thang đo trong phân tích SEM, dựa trên so sánh căn bậc hai của AVE với các hệ số tương quan giữa các biến tiềm ẩn.
1. Lý thuyết về tiêu chí Fornell và Larcker
Trong nghiên cứu định lượng, có nhiều phương pháp được sử dụng nhằm đánh giá tính phân biệt của thang đo, trong đó tiêu chí Fornell và Larcker do hai tác giả Fornell và Larcker đề xuất lần đầu vào năm 1981 là một trong những phương pháp phổ biến. Cho đến nay, phương pháp này thường được xem là cách tiếp cận truyền thống trong đánh giá tính phân biệt và vẫn được áp dụng rộng rãi trong các nghiên cứu khoa học, luận văn và luận án ở nhiều bậc học khác nhau.
Phương pháp Fornell và Larcker được xây dựng dựa trên việc so sánh căn bậc hai của phương sai trích trung bình AVE, ký hiệu là SQRT(AVE), của một biến tiềm ẩn với các hệ số tương quan giữa biến tiềm ẩn đó và các biến tiềm ẩn còn lại trong mô hình. Trong đó, AVE (average variance extracted) phản ánh mức độ mà biến tiềm ẩn giải thích trung bình cho các biến quan sát dùng để đo lường nó. Khi giá trị SQRT(AVE) của một biến tiềm ẩn lớn hơn tất cả các hệ số tương quan giữa biến đó với các biến tiềm ẩn khác, có thể kết luận rằng thang đo đạt yêu cầu về tính phân biệt. Khái niệm và cách đánh giá chỉ số AVE được trình bày chi tiết trong các nghiên cứu Đánh giá tính hội tụ thang đo bằng Average Variance Extracted AVE.
2. Đánh giá tính phân biệt bằng tiêu chí Fornell–Larcker
Giả định nghiên cứu xem xét mối quan hệ giữa ba khái niệm A, B và C, trong đó cả ba đều được đo lường bằng mô hình đo lường phản xạ. Một bước quan trọng trong quá trình phân tích là đánh giá giá trị phân biệt của từng thang đo nhằm đảm bảo rằng mỗi khái niệm tiềm ẩn là khác biệt so với các khái niệm còn lại. Quá trình đánh giá được minh họa bắt đầu với các biến quan sát của biến tiềm ẩn A. Để thực hiện, cần xây dựng ma trận tương quan giữa ba biến tiềm ẩn A, B và C, đồng thời xác định giá trị căn bậc hai của phương sai trích trung bình (SQRT(AVE)) của thang đo A. Bảng dưới đây trình bày cấu trúc bảng Fornell–Larcker, một định dạng được sử dụng phổ biến trong các phần mềm phân tích mô hình cấu trúc tuyến tính (SEM).
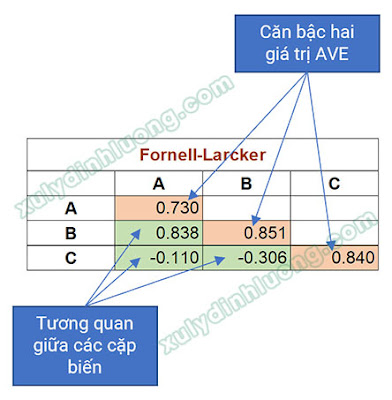
Bảng được trình bày dưới dạng ma trận, trong đó hàng và cột đầu tiên thể hiện tên các biến tiềm ẩn đại diện cho các thang đo tương ứng, cụ thể là A, B và C. Các ô giá trị bên trong ma trận bao gồm hai nhóm thông tin: (1) các giá trị SQRT(AVE) của từng biến tiềm ẩn và (2) các hệ số tương quan giữa các cặp biến tiềm ẩn.
– Đối với các giá trị SQRT(AVE): giá trị 0.730 xuất hiện tại giao điểm cột A và hàng A, đại diện cho SQRT(AVE) của biến A. Tương tự, các giá trị 0.851 và 0.840 lần lượt phản ánh SQRT(AVE) của các biến B và C.
– Đối với các hệ số tương quan: giá trị 0.838 biểu thị mức độ tương quan giữa biến A và biến B; giá trị -0.110 thể hiện tương quan giữa biến A và biến C; và giá trị -0.306 phản ánh tương quan giữa biến B và biến C.
Cách diễn giải bảng Fornell và Larcker:
Được thực hiện bằng việc so sánh căn bậc hai của AVE (SQRT(AVE)) của biến tiềm ẩn A với các hệ số tương quan giữa A và các biến tiềm ẩn khác như B và C. Cụ thể, nếu SQRT(AVE) của A lớn hơn giá trị tuyệt đối của hệ số tương quan giữa A với B và giữa A với C, thì thang đo của A được xem là đạt giá trị phân biệt. Ngược lại, nếu SQRT(AVE) của A nhỏ hơn ít nhất một trong các hệ số tương quan nói trên, thì giá trị phân biệt của thang đo A không được đảm bảo.
Trong ví dụ minh họa, SQRT(AVE) của biến A đạt giá trị 0.730. Mặc dù giá trị này lớn hơn 0.110, là giá trị tuyệt đối của hệ số tương quan giữa A và C, nhưng lại nhỏ hơn 0.838, là giá trị tuyệt đối của hệ số tương quan giữa A và B. Do đó, có thể kết luận rằng thang đo của A không đạt giá trị phân biệt; cụ thể, hai biến tiềm ẩn A và B vi phạm yêu cầu về giá trị phân biệt.
Lập luận của Fornell và Larcker (1981) dựa trên giả định rằng khi một biến tiềm ẩn A tác động đến các biến quan sát của nó, biến A sẽ truyền tải và chia sẻ một phần phương sai của mình cho các chỉ báo này. Đồng thời, A cũng có mối quan hệ hoặc tác động nhất định đến các biến tiềm ẩn khác như B và C, dẫn đến việc A tiếp tục chia sẻ phương sai với các biến này. Theo đó, nếu mức độ phương sai mà A chia sẻ với các chỉ báo của chính nó, được đại diện bởi căn bậc hai của AVE, lớn hơn mức độ phương sai mà A chia sẻ với các biến tiềm ẩn khác như C, thì thang đo của A được xem là đạt giá trị phân biệt đối với C, và ngược lại.
Tuy nhiên, Henseler và cộng sự (2015) đã cung cấp các bằng chứng thực nghiệm cho thấy tiêu chí Fornell và Larcker (1981) không đánh giá đầy đủ và chính xác giá trị phân biệt của thang đo, do còn tồn tại những hạn chế về cơ sở thống kê suy diễn. Trên cơ sở đó, nhóm tác giả đã đề xuất một phương pháp thay thế nhằm khắc phục các hạn chế này, được gọi là chỉ số tương quan Heterotrait-Monotrait, viết tắt là HTMT. Phương pháp HTMT sau đó đã được cộng đồng nghiên cứu chấp nhận và sử dụng rộng rãi trong việc đánh giá giá trị phân biệt của thang đo. Nội dung chi tiết về chỉ số này sẽ được trình bày trong bài viết Đánh giá tính phân biệt thang đo bằng chỉ số HTMT.
Bảng Fornell-Larcker có thể được hiển thị trực tiếp trên giao diện phần mềm SmartPLS 4:
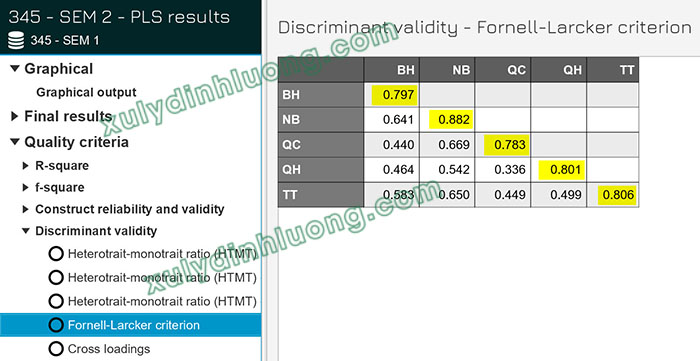
Ngoài ra, bảng Fornell-Larcker cũng có thể được tạo ra thông qua plugin sử dụng trong phần mềm AMOS, với lưu ý rằng tệp dữ liệu sử dụng trong AMOS khác với tệp dữ liệu dùng trong SmartPLS:
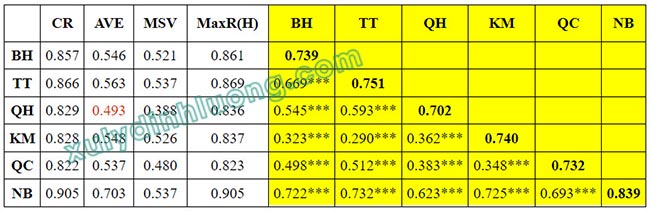
Xem thêm: Đánh giá tính phân biệt qua bảng Cross-Loading trong SMARTPLS
Xem thêm: Đánh giá tính phân biệt thang đo bằng HTMT trong SMARTPLS
