Trong bài viết Đánh giá tính phân biệt thang đo bằng bảng Fornell and Larcker, chúng ta đã tiếp cận một phương pháp phổ biến nhằm xem xét mức độ phân biệt giữa các thang đo hoặc tập hợp các chỉ báo. Tuy nhiên, Henseler và cộng sự (2015) đã cung cấp các bằng chứng thực nghiệm cho thấy phương pháp do Fornell và Larcker (1981) đề xuất không đảm bảo khả năng đánh giá chính xác giá trị phân biệt của thang đo trong nhiều trường hợp. Trên cơ sở đó, các tác giả đã đề xuất một phương pháp thay thế và hiện nay được chấp nhận rộng rãi trong nghiên cứu thực nghiệm, được gọi là chỉ số tương quan Heterotrait-Monotrait (Heterotrait-Monotrait Ratio of Correlations), viết tắt là HTMT.
1. Cơ sở lý thuyết của việc xây dựng chỉ số HTMT
Chỉ số HTMT được xây dựng dựa trên nền tảng của ma trận multitrait-multimethod (MTMM) do Campbell và Fiske (1959) đề xuất. Ma trận MTMM yêu cầu tối thiểu hai tập chỉ báo được sử dụng để đo lường hai biến tiềm ẩn khác nhau (nhiều đặc tính – multiple traits), trong đó mỗi tập chỉ báo có số lượng tương đương nhau, tạo thành một ma trận cân bằng (symmetric matrix). Về bản chất, ma trận này chính là ma trận tương quan giữa các chỉ báo của các biến tiềm ẩn. Trước khi trình bày công thức tính toán chỉ số HTMT, việc minh họa cấu trúc của ma trận MTMM đối với hai khái niệm A và B như thể hiện trong hình dưới đây sẽ giúp làm rõ cơ sở lý thuyết của chỉ số này.
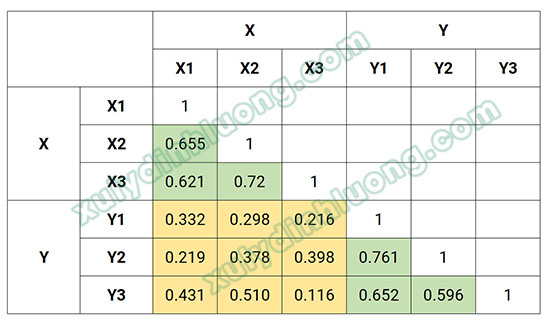
Bảng minh họa trình bày ma trận tương quan giữa sáu chỉ báo được sử dụng để đo lường hai biến tiềm ẩn X và Y. Các hệ số tương quan trong ma trận này được phân thành ba nhóm khác nhau, được thể hiện bằng hai vùng màu xanh và một vùng màu vàng.
Các hệ số tương quan nằm trong vùng màu xanh đại diện cho tương quan nội bộ giữa các chỉ báo đo lường cùng một biến tiềm ẩn, còn được gọi là tương quan giữa các chỉ báo (inter-item correlations), và được định danh là monotrait-heteromethod correlations. Trong khi đó, các hệ số tương quan nằm trong vùng màu vàng phản ánh mối tương quan chéo giữa các chỉ báo thuộc hai biến tiềm ẩn khác nhau, được gọi là heterotrait-heteromethod correlations.
2. Đánh giá giá trị phân biệt thông qua chỉ số HTMT
Việc đánh giá giá trị phân biệt được xây dựng trên cơ sở lập luận rằng: trung bình các hệ số tương quan giữa các chỉ báo thuộc cùng một thang đo càng lớn so với trung bình các hệ số tương quan giữa các chỉ báo của các thang đo khác nhau thì mức độ phân biệt càng được đảm bảo. Khi trung bình hệ số tương quan trong nội bộ một thang đo càng cao, điều này cho thấy biến tiềm ẩn tương ứng chia sẻ mức độ biến thiên lớn hơn giữa các chỉ báo của chính nó. Ngược lại, nếu trung bình các hệ số tương quan chéo giữa các thang đo càng thấp thì biến tiềm ẩn đó càng ít chia sẻ sự biến động với các biến tiềm ẩn khác. Trong trường hợp này, các chỉ báo của các biến tiềm ẩn khác nhau sẽ đạt được giá trị phân biệt.
Dựa trên lập luận này, Henseler và cộng sự (2015) đã đề xuất chỉ số HTMT (Heterotrait–Monotrait ratio) nhằm đánh giá giá trị phân biệt giữa từng cặp thang đo. Công thức tính HTMT cho cặp biến tiềm ẩn i và j được xác định như sau:
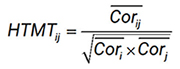
Trong đó:
- HTMTij là giá trị HTMT của cặp biến tiềm ẩn i và j.
- Corij là trung bình cộng các hệ số tương quan của tất cả các cặp biến quan sát thuộc hai biến tiềm ẩn i và j.
- Cori là trung bình cộng các hệ số tương quan giữa các cặp biến quan sát của biến tiềm ẩn i.
- Corj là trung bình cộng các hệ số tương quan giữa các cặp biến quan sát của biến tiềm ẩn j.
Để minh họa rõ hơn cách tính chỉ số HTMT, xét ví dụ cặp biến X và Y được trình bày trong bảng dữ liệu ở trên. Các giá trị trung bình hệ số tương quan được tính như sau:
- CorXY = (0.332 + 0.298 + 0.216 + 0.219 + 0.378 + 0.398 + 0.431 + 0.510 + 0.116) / 9 = 0.322
- CorX = (0.655 + 0.621 + 0.720) / 3 = 0.666
- CorY = (0.761 + 0.652 + 0.596) / 3 = 0.670
Thay các giá trị trên vào công thức HTMT, ta thu được kết quả:
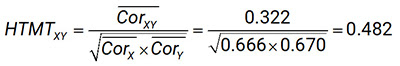
Kết quả cho thấy trung bình các hệ số tương quan chéo giữa các chỉ báo của hai biến tiềm ẩn X và Y cần nhỏ hơn so với trung bình nhân các hệ số tương quan trong nội bộ từng thang đo X và Y. Khi điều kiện này được thỏa mãn, hai biến tiềm ẩn chủ yếu chia sẻ sự biến động trong phạm vi các chỉ báo của chính thang đo tương ứng, đồng thời ít chia sẻ sự biến động lẫn nhau. Khi đó, tập hợp các chỉ báo của biến tiềm ẩn X sẽ đảm bảo giá trị phân biệt so với tập hợp các chỉ báo của biến tiềm ẩn Y.
Henseler và cộng sự (2015) đề xuất hai ngưỡng để đánh giá giá trị phân biệt giữa các biến tiềm ẩn i và j. Cụ thể:
- Nếu HTMTij lớn hơn 0.9 thì khó có thể khẳng định tồn tại giá trị phân biệt giữa hai biến tiềm ẩn, cho thấy các tập chỉ báo có mức độ tương đồng cao.
- Ngược lại, nếu HTMTij nhỏ hơn hoặc bằng 0.85 thì có thể kết luận rằng giá trị phân biệt giữa hai biến tiềm ẩn được đảm bảo.
Dựa trên kết quả tính toán trong ví dụ trên, chỉ số HTMTXY bằng 0.482, nhỏ hơn ngưỡng 0.85, do đó có thể kết luận rằng hai biến tiềm ẩn X và Y đạt được giá trị phân biệt. Trong trường hợp mô hình nghiên cứu bao gồm thêm các biến tiềm ẩn khác như M và N (đều thuộc mô hình đo lường phản xạ), việc đánh giá giá trị phân biệt sẽ được thực hiện thông qua việc xem xét chỉ số HTMT cho từng cặp biến tiềm ẩn, bao gồm X–Y, X–M, X–N, Y–M, Y–N và M–N.
3. Cách đọc kết quả HTMT trên SMARTPLS 3 và SMARTPLS 4
Mặc dù giao diện hiển thị kết quả của SMARTPLS 3 và SMARTPLS 4 có sự khác biệt nhất định, chỉ số HTMT luôn được cung cấp trong kết quả phân tích PLS Algorithm. Theo khuyến nghị trong các nghiên cứu phương pháp luận, ngưỡng chấp nhận của HTMT là không vượt quá 0.9.
- Cụ thể, khi giá trị HTMT của một cặp biến nhỏ hơn 0.85, SMARTPLS sẽ hiển thị màu xanh, phản ánh mức độ phân biệt rất tốt;
- Khi giá trị HTMT nằm trong khoảng từ 0.85 đến 0.9, kết quả được hiển thị bằng màu đen và vẫn được xem là chấp nhận được;
- Trong trường hợp giá trị HTMT lớn hơn 0.9, phần mềm sẽ hiển thị màu đỏ, cho thấy sự vi phạm tính phân biệt.
Để xem bảng HTMT trong SMARTPLS 3, người nghiên cứu tiến hành chạy PLS Algorithm, sau đó chọn mục Discriminant Validity để đánh giá mô hình đo lường.

Tiếp theo, lựa chọn thẻ thứ ba là Heterotrait-Monotrait Ratio (HTMT).
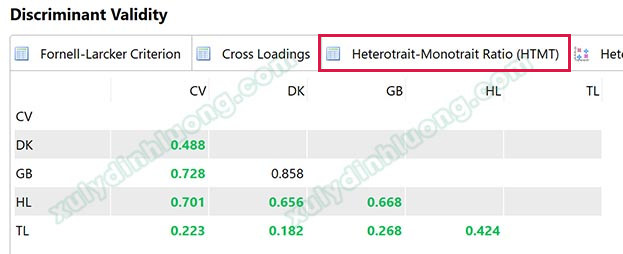
→ Kết quả từ ví dụ minh họa cho thấy tất cả các giá trị HTMT đều nhỏ hơn 0.9, qua đó khẳng định rằng tính phân biệt của mô hình đo lường được đảm bảo.
Đối với SMARTPLS 4, để xem kết quả bảng HTMT, từ kết quả phân tích PLS-SEM Algorithm, người dùng chọn mục Discriminant Validity và tiếp tục lựa chọn Heterotrait-Monotrait Ratio (HTMT) – Matrix để đánh giá mô hình đo lường.
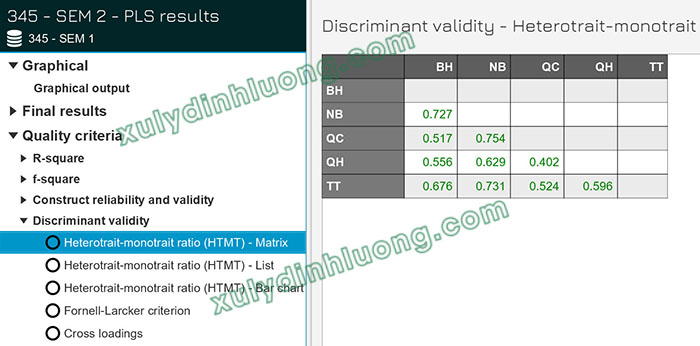
→ Kết quả từ ví dụ thực hành trong SMARTPLS 4 cũng cho thấy toàn bộ giá trị HTMT đều nhỏ hơn 0.9, chứng tỏ tính phân biệt của mô hình được đảm bảo. Cần lưu ý rằng dữ liệu sử dụng trong các ví dụ minh họa ở hai phiên bản SMARTPLS 3 và SMARTPLS 4 là khác nhau; trong trường hợp sử dụng cùng một bộ dữ liệu, kết quả HTMT thu được ở các phiên bản phần mềm sẽ là tương đồng.
Xem thêm: Đánh giá tính phân biệt thang đo bằng bảng Fornell and Larcker
Xem thêm: Đánh giá tính phân biệt qua bảng Cross-Loading trong SMARTPLS
