Đánh giá cộng tuyến trong phân tích SEM bằng AMOS

Một hạn chế đáng chú ý của phần mềm AMOS là không cung cấp các chỉ số chẩn đoán nhằm đánh giá hiện tượng cộng tuyến trong mô hình SEM, chẳng hạn như hệ số phóng đại phương sai (VIF), chỉ số dung sai (Tolerance) và các thước đo tương tự. Do đó, trong trường hợp mô hình tồn tại vấn đề cộng tuyến dẫn đến sai lệch trong các ước lượng của phân tích SEM, nhà nghiên cứu gặp nhiều khó khăn trong việc xác định nguyên nhân phát sinh sai lệch này.

1. Hệ quả của hiện tượng cộng tuyến và đa cộng tuyến trong mô hình SEM

Cơ sở lý thuyết liên quan đến cộng tuyến và đa cộng tuyến có thể tham khảo tại các tài liệu chuyên sâu Đa cộng tuyến: Nguyên nhân, hậu quả, dấu hiệu và cách khắc phục..

• Cộng tuyến (Collinearity) được hiểu là hiện tượng xảy ra khi hai biến độc lập có mối tương quan tuyến tính rất mạnh với nhau.

• Đa cộng tuyến (Multicollinearity) xảy ra khi từ ba biến độc lập trở lên có mối tương quan tuyến tính chặt chẽ, và có thể xem đây là dạng mở rộng của hiện tượng cộng tuyến.

Trong cả mô hình hồi quy tuyến tính truyền thống lẫn mô hình cấu trúc tuyến tính SEM, sự tồn tại của cộng tuyến đều có thể dẫn đến những hệ quả nghiêm trọng.

• Cụ thể, các mối quan hệ vốn có ý nghĩa thống kê có thể trở nên không có ý nghĩa, trong khi các quan hệ không có ý nghĩa lại được ước lượng là có ý nghĩa.
• Dấu của hệ số tác động có thể bị đảo chiều từ dương sang âm hoặc ngược lại;
• Mức độ tác động của các biến có thể bị đánh giá sai lệch, từ mạnh thành yếu hoặc từ yếu thành mạnh.
• Ngoài ra, có thể xuất hiện các giá trị bất hợp lý như hệ số hồi quy chuẩn hóa vượt quá ngưỡng 1 hoặc hệ số xác định R² lớn hơn 1.

Những hệ quả này cho thấy rằng nếu không kiểm soát và đánh giá đầy đủ hiện tượng cộng tuyến, kết quả phân tích, diễn giải và kết luận của mô hình SEM có nguy cơ sai lệch nghiêm trọng.

2. Đánh giá hiện tượng đa cộng tuyến trong phân tích SEM bằng AMOS

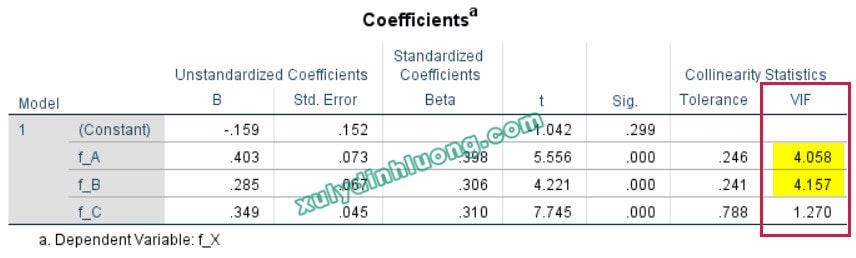
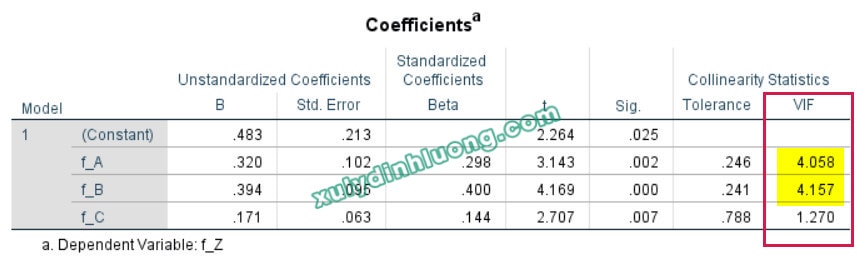
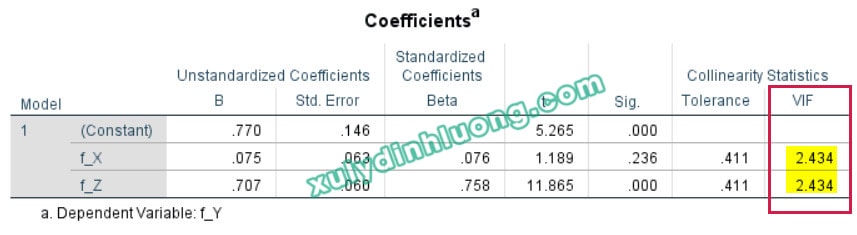
Trong quá trình thực hiện phân tích mô hình cấu trúc tuyến tính (SEM), khi xuất hiện một số dấu hiệu bất thường như hệ số hồi quy chuẩn hóa vượt quá giá trị 1, hệ số xác định R bình phương lớn hơn 1, hoặc mối quan hệ tác động theo lý thuyết được giả định là cùng chiều nhưng kết quả ước lượng lại cho thấy tác động ngược chiều với cường độ rất lớn, thì có thể suy luận với xác suất cao rằng mô hình đang gặp phải vấn đề đa cộng tuyến. Chẳng hạn, trong ví dụ minh họa từ bộ dữ liệu bên dưới, có tới bốn hệ số tác động chuẩn hóa vượt ngưỡng 1 và giá trị R bình phương của biến X cũng lớn hơn 1.

Do phần mềm AMOS không cung cấp trực tiếp các chỉ số như VIF nhằm phát hiện hiện tượng đa cộng tuyến trong mô hình SEM, nên cần sử dụng phương pháp hồi quy tuyến tính trong SPSS như một công cụ hỗ trợ để đánh giá vấn đề này. Quy trình thực hiện được tiến hành theo các bước sau.

Bước 1: Chuyển đổi mô hình SEM phức tạp thành các mô hình hồi quy tuyến tính đơn giản

Về mặt lý thuyết, đa cộng tuyến là hiện tượng xảy ra giữa các biến độc lập. Tuy nhiên, trong bối cảnh một mô hình SEM phức tạp bao gồm nhiều loại biến như biến độc lập, biến trung gian, biến điều tiết và biến phụ thuộc, vấn đề đặt ra là phạm vi xem xét đa cộng tuyến có chỉ giới hạn giữa các biến độc lập hay không.

Các biến độc lập được đề cập ở đây cần được xem xét trong từng ngữ cảnh cụ thể, tức là các biến cùng tác động lên một biến khác trong mô hình. Do đó, cần tách mô hình SEM tổng thể thành các mô hình hồi quy tuyến tính đơn giản, sau đó đánh giá hiện tượng đa cộng tuyến giữa các biến độc lập trong từng mô hình hồi quy này.

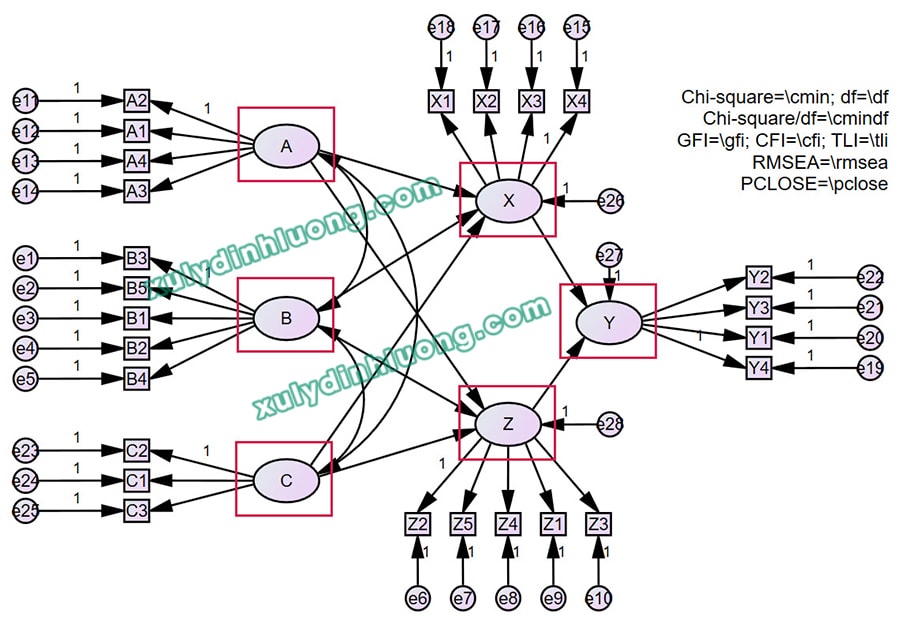
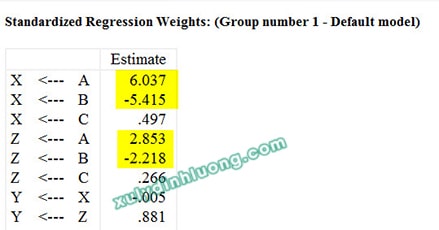
Xét mô hình minh họa từ kết quả phân tích ở trên:

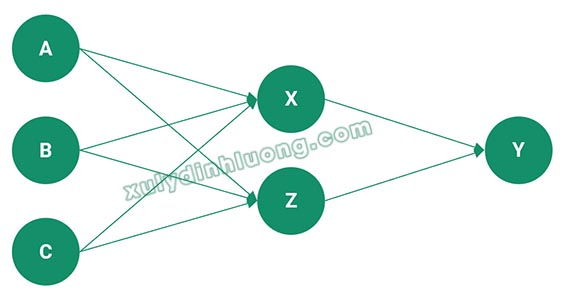
Trong bối cảnh mô hình SEM tổng thể, các biến A, B, C được xem là biến độc lập, các biến X và Z đóng vai trò biến trung gian, còn biến Y là biến phụ thuộc. Tiếp theo, mô hình SEM phức tạp này được chuyển đổi thành các mô hình hồi quy tuyến tính đơn giản.

Hồi quy tuyến tính là mô hình trong đó một hoặc nhiều biến độc lập cùng tác động lên một biến phụ thuộc. Theo đó, trong một mô hình SEM, số lượng biến đóng vai trò phụ thuộc sẽ tương ứng với số lượng mô hình hồi quy tuyến tính cần được xây dựng. Cần lưu ý rằng biến trung gian là loại biến có vai trò kép, vừa là biến phụ thuộc trong một mối quan hệ, vừa là biến độc lập trong mối quan hệ khác.

Các biến được xác định là biến phụ thuộc trong mô hình SEM là những biến nhận mũi tên tác động hướng vào. Cụ thể, trong mô hình ví dụ, các biến nhận mũi tên hướng vào bao gồm X, Z và Y. Như vậy, mô hình SEM này có ba biến giữ vai trò phụ thuộc, tương ứng với ba mô hình hồi quy tuyến tính đơn giản được hình thành như sau:

• Mô hình hồi quy 1: các biến độc lập A, B, C tác động lên biến phụ thuộc X;

• Mô hình hồi quy 2: các biến độc lập A, B, C tác động lên biến phụ thuộc Z;

• Mô hình hồi quy 3: các biến độc lập X, Z tác động lên biến phụ thuộc Y.

Nếu bạn muốn, mình có thể tiếp tục viết Bước 2 (chạy hồi quy trên SPSS và đọc chỉ số VIF, Tolerance) theo cùng phong cách học thuật để bạn ghép thẳng vào luận văn hoặc bài báo.

Bước 2: Xác định phương pháp đánh giá hiện tượng đa cộng tuyến

Từ kết quả của bước trước, nghiên cứu đã xác định được ba mô hình hồi quy đơn giản. Việc đánh giá hiện tượng đa cộng tuyến được tiến hành giữa các biến độc lập nằm trong cùng một mô hình hồi quy đơn giản nhằm đảm bảo các giả định của mô hình hồi quy tuyến tính được thỏa mãn.

Cụ thể, hiện tượng đa cộng tuyến được xem xét đối với các nhóm biến sau:

(i) các biến A, B, C trong mô hình hồi quy thứ nhất;

(ii) các biến A, B, C trong mô hình hồi quy thứ hai;

(iii) các biến X và Z trong mô hình hồi quy thứ ba.

Do các biến độc lập trong mô hình hồi quy thứ nhất và thứ hai là tương đồng, việc đánh giá hiện tượng đa cộng tuyến chỉ cần thực hiện một lần cho nhóm biến này. Như vậy, để kiểm tra hiện tượng đa cộng tuyến trong mô hình SEM tổng thể ban đầu, nghiên cứu cần tiến hành đánh giá đối với hai nhóm biến độc lập, bao gồm:

Nhóm biến A, B, C

Nhóm biến X, Z.

Bước 3: Chuẩn bị dữ liệu các biến phục vụ phân tích mô hình hồi quy đơn giản

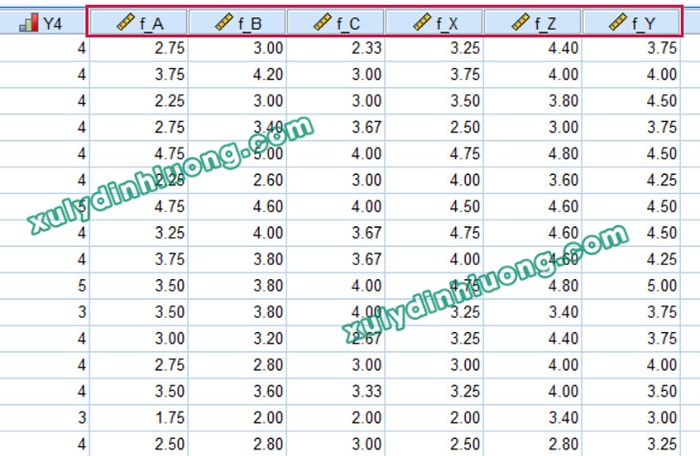
Trong mô hình SEM được ước lượng bằng phần mềm AMOS, các biến tiềm ẩn được phần mềm tự động tính toán dựa trên dữ liệu của các biến quan sát thể hiện trên sơ đồ mô hình, do đó không tồn tại bộ dữ liệu riêng cho các biến tiềm ẩn. Ngược lại, khi thực hiện phân tích hồi quy trên SPSS, người nghiên cứu cần phải xây dựng dữ liệu cho các biến tiềm ẩn nhằm đưa vào quá trình khai báo và phân tích mô hình.

Dữ liệu của các biến tiềm ẩn, hay còn gọi là biến đại diện, thường được tính toán theo hai phương pháp phổ biến là lấy tổng hoặc lấy giá trị trung bình của các biến quan sát thành phần, bạn tham khảo hai cách thực hiện ở bài viết này. Khi thực hiện tính toán biến đại diện, cần lưu ý loại bỏ các biến quan sát đã bị loại bỏ trong các bước phân tích SEM trước đó như kiểm định độ tin cậy Cronbach’s Alpha, phân tích nhân tố khám phá EFA hoặc phân tích nhân tố khẳng định CFA.

Trong quá trình đặt tên cho các biến đại diện trong bộ dữ liệu SPSS, cần đảm bảo tên biến không trùng với tên các biến tiềm ẩn đã được khai báo trong sơ đồ AMOS. Nguyên nhân là do các biến tiềm ẩn trong AMOS được phần mềm tính toán trực tiếp từ dữ liệu biến quan sát mà không yêu cầu dữ liệu đầu vào riêng. Việc tạo biến đại diện trùng tên trong SPSS có thể gây xung đột với cơ chế tính toán biến tiềm ẩn của AMOS. Do đó, một giải pháp thường được áp dụng là bổ sung tiền tố cho tên biến đại diện trong SPSS, chẳng hạn như thêm tiền tố f_ vào trước tên biến, nhằm phân biệt rõ ràng với tên biến tiềm ẩn trên sơ đồ AMOS.