Các phương pháp xử lý mô hình biến bậc hai, biến bậc cao trong SmartPLS 3

Để nắm bắt đầy đủ nội dung của bài viết này, trước hết người đọc cần hiểu rõ cơ sở lý thuyết về mô hình bậc cao, đã được trình bày trong bài viết về mô hình thành phần thứ bậc và mô hình bậc cao trong PLS-SEM. Trong quá trình xử lý các vấn đề đo lường liên quan đến mô hình thành phần thứ bậc trong PLS-SEM, các nhà nghiên cứu thường dựa vào hai cách tiếp cận chủ yếu nhằm đặc tả mô hình trong phân tích đường dẫn PLS, bao gồm: (1) phương pháp biến quan sát lặp lại và (2) phương pháp hai giai đoạn. Hai phương pháp này đã được đề xuất và thảo luận rộng rãi trong các nghiên cứu trước đây của Becker và cộng sự (2012), Ringle và cộng sự (2012) cũng như Wetzels và cộng sự (2009).

1. Phương pháp biến quan sát lặp lại

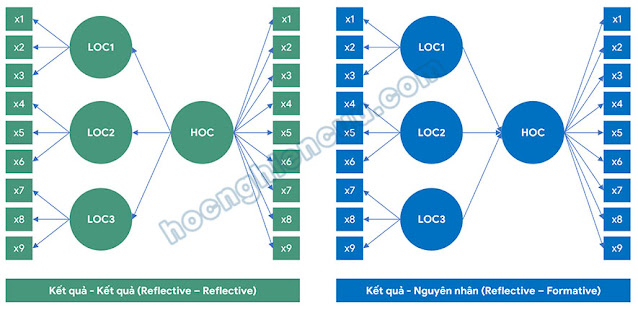
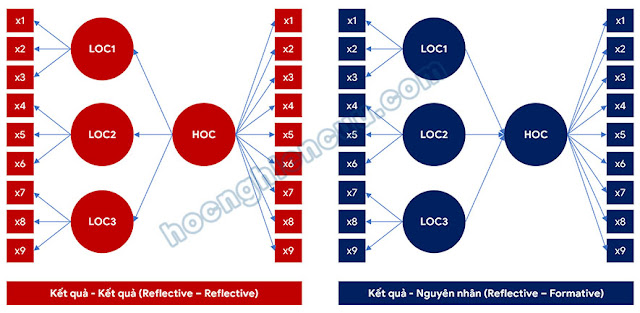
Trong phương pháp tiếp cận biến quan sát lặp lại, toàn bộ các biến quan sát của các cấu trúc bậc thấp được gán đồng thời cho mô hình đo lường của cấu trúc bậc cao. Cách tiếp cận này được đề xuất trong các nghiên cứu nền tảng của Lohmöller (1989) và Wold (1982). Trong các ví dụ minh họa về mô hình bậc hai, phương pháp biến quan sát lặp lại sử dụng các biến quan sát từ x1 đến x9 của các cấu trúc bậc thấp để xây dựng mô hình đo lường cho cấu trúc bậc cao. Theo đó, mỗi biến quan sát được sử dụng hai lần, một lần để đo lường cấu trúc bậc thấp và một lần để đo lường cấu trúc bậc cao. Do đó, nếu bất kỳ biến quan sát nào của cấu trúc bậc thấp bị loại bỏ do không đáp ứng các tiêu chuẩn đánh giá, thì biến quan sát đó cũng cần được loại bỏ khỏi mô hình đo lường của cấu trúc bậc cao.

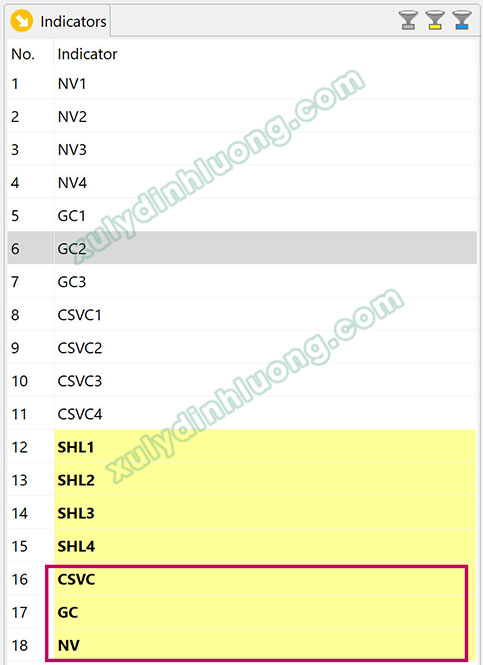
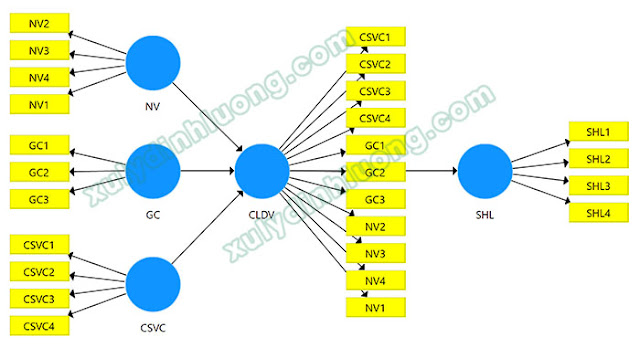
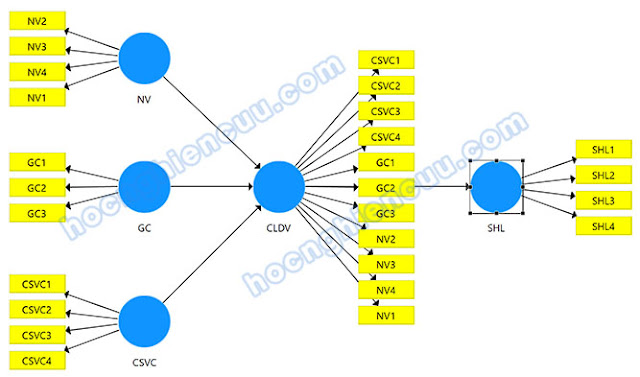
Xét ví dụ minh họa trên sơ đồ mô hình trong phần mềm SmartPLS, cấu trúc Chất lượng dịch vụ được xem là cấu trúc bậc cao và được đo lường thông qua ba cấu trúc bậc thấp gồm Nhân viên, Giá cả và Cơ sở vật chất. Khi áp dụng phương pháp biến quan sát lặp lại, toàn bộ 11 biến quan sát thuộc ba cấu trúc bậc thấp này sẽ được kéo và gán trực tiếp vào cấu trúc bậc hai Chất lượng dịch vụ để thiết lập mô hình đo lường.

Đánh giá ưu điểm và hạn chế của phương pháp biến quan sát lặp lại trong SmartPLS cho thấy phương pháp này có những đặc điểm sau.

– Về ưu điểm, phương pháp có cách triển khai tương đối đơn giản và dễ thực hiện. Các chỉ số đánh giá mô hình đo lường và mô hình cấu trúc về cơ bản đều có thể được tính toán đầy đủ, cho phép nhà nghiên cứu đưa ra kết luận về mô hình mà không cần tiến hành thêm các phân tích bổ sung. Đặc biệt, trong trường hợp mối quan hệ giữa cấu trúc bậc cao và cấu trúc bậc thấp được mô hình hóa dưới dạng kết quả, việc áp dụng duy nhất phương pháp này là đủ để đánh giá toàn bộ mô hình nghiên cứu.

– Tuy nhiên, phương pháp biến quan sát lặp lại cũng tồn tại một số hạn chế nhất định. Khi mối quan hệ giữa cấu trúc bậc cao và cấu trúc bậc thấp mang tính nguyên nhân, hoặc khi nhà nghiên cứu có nhu cầu đánh giá sâu hơn các đặc điểm đo lường của cấu trúc bậc cao, nhiều chỉ số đánh giá không thể được phần mềm SmartPLS tính toán. Điều này buộc nhà nghiên cứu phải bỏ qua hoặc hạn chế phần đánh giá chi tiết đối với cấu trúc bậc cao trong mô hình.

2. Phương pháp tiếp cận hai giai đoạn (Two-stage approach)

Đối với mô hình cấu trúc phân cấp (Hierarchical Component Model – HCM) dưới dạng kết quả – kết quả hoặc nguyên nhân – kết quả, bên cạnh việc đánh giá mô hình đo lường của các cấu trúc bậc thấp (Lower-order Components – LOC), nhà nghiên cứu cần tiến hành đánh giá cả mô hình đo lường của cấu trúc bậc cao (Higher-order Component – HOC). Việc đánh giá mô hình đo lường của HOC tập trung vào mối quan hệ giữa HOC và các LOC cấu thành, thay vì mối quan hệ giữa HOC và các biến quan sát được gán trực tiếp vào nó.

Trong phương pháp tiếp cận biến quan sát lặp lại, phần lớn các chỉ số đánh giá mô hình đo lường như Cronbach’s Alpha, độ tin cậy tổng hợp (CR), phương sai trích trung bình (AVE), tiêu chí Fornell–Larcker, chỉ số HTMT,… khi xem xét độ tin cậy, giá trị hội tụ và giá trị phân biệt chỉ thực sự phù hợp để đánh giá các LOC. Mặc dù kết quả từ phân tích PLS Algorithm hoặc Bootstrapping trên phần mềm SmartPLS vẫn cung cấp các chỉ số Cronbach’s Alpha, CR và AVE cho HOC trong phần output, nhưng các giá trị này được tính toán dựa trên các biến quan sát lặp lại của các LOC được kéo thả vào HOC, chứ không phản ánh trực tiếp mối quan hệ đo lường giữa HOC và các LOC.

Xuất phát từ hạn chế này, kỹ thuật tiếp cận hai giai đoạn được đề xuất nhằm cho phép đánh giá mô hình đo lường của HOC một cách chính xác và phù hợp hơn. Phương pháp này được gọi là tiếp cận hai giai đoạn do quy trình thực hiện được chia thành hai bước phân tích riêng biệt.

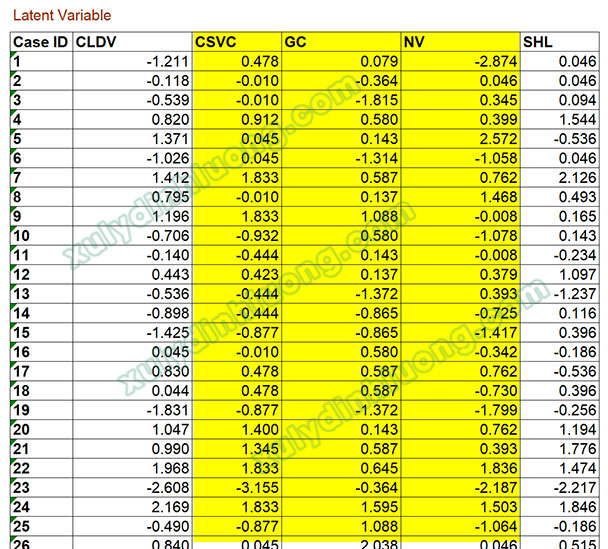
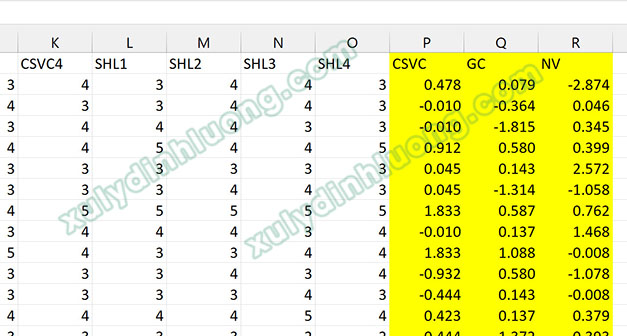
Ở giai đoạn thứ nhất, mô hình được ước lượng bằng phương pháp biến quan sát lặp lại nhằm thu được điểm số của các LOC. Sau đó, các điểm số LOC này được trích xuất và lưu lại dưới dạng các biến mới trong bộ dữ liệu, phục vụ cho giai đoạn phân tích tiếp theo. Cách tiếp cận này cho phép chuyển đổi một cấu trúc bậc hai phức tạp thành các cấu trúc bậc một đơn giản hơn.

Ở giai đoạn thứ hai, một sơ đồ mô hình mới được xây dựng dựa trên bộ dữ liệu đã bao gồm các biến điểm số LOC. Trong mô hình này, các LOC đóng vai trò như các biến quan sát, trong khi HOC được xem như một biến tiềm ẩn bậc một. Việc đánh giá mô hình lúc này được thực hiện tương tự như đối với một mô hình cấu trúc bậc một thông thường.

Về ưu điểm, phương pháp tiếp cận hai giai đoạn cho phép thu được đầy đủ các chỉ số cần thiết để đánh giá mô hình đo lường của HOC và có thể áp dụng cho mọi dạng mô hình HCM mà không gặp trở ngại về mặt kỹ thuật.

Tuy nhiên, phương pháp này cũng tồn tại một số hạn chế, bao gồm quy trình thực hiện tương đối phức tạp và không cho phép đánh giá đồng thời mô hình đo lường của các LOC trong cùng một lần phân tích.

3. Quy trình xử lý biến bậc hai trong SMARTPLS

Hair và cộng sự (2018) đề xuất rằng phương pháp tiếp cận biến quan sát lặp lại nên được ưu tiên áp dụng trong trường hợp mối quan hệ giữa cấu trúc bậc cao (HOC) và cấu trúc bậc thấp (LOC) là mối quan hệ kết quả, trong khi phương pháp hai giai đoạn phù hợp hơn khi HOC và LOC có mối quan hệ nhân quả. Tuy nhiên, do mỗi phương pháp đều tồn tại những hạn chế nhất định, việc kết hợp cả hai cách tiếp cận được xem là cần thiết nhằm đảm bảo đánh giá mô hình một cách toàn diện và chặt chẽ hơn.

Ở giai đoạn thứ nhất của kỹ thuật hai giai đoạn, thay vì chỉ trích xuất trọng số của các LOC thông qua phương pháp biến quan sát lặp lại, nghiên cứu tiến hành đánh giá đầy đủ mô hình đo lường của các LOC. Sau đó, ở giai đoạn thứ hai, mô hình đo lường của HOC được tiếp tục kiểm định. Như vậy, quy trình xử lý biến bậc hai được đề xuất trong SMARTPLS bao gồm các bước sau:

Bước 1 – Áp dụng kỹ thuật biến quan sát lặp lại. Trong bước này, hai nội dung chính được thực hiện:

• Đánh giá mô hình đo lường của các LOC. Tùy thuộc vào bản chất của mô hình là dạng kết quả hay dạng nguyên nhân, các tiêu chí đánh giá phù hợp sẽ được sử dụng tương ứng. Tham khảo thêm các nội dung về đánh giá mô hình đo lường dạng kết quả trên SMARTPLS và đánh giá mô hình đo lường dạng nguyên nhân trên SMARTPLS.

• Trích xuất các trọng số của LOC để bổ sung vào bộ dữ liệu phục vụ cho giai đoạn phân tích tiếp theo.

Bước 2 – Thực hiện giai đoạn hai của kỹ thuật hai giai đoạn. Trong bước này, hai nội dung chính được tiến hành:

• Xây dựng sơ đồ mới biểu diễn các biến LOC được tính toán dựa trên trọng số nhân tố, đồng thời đánh giá mô hình đo lường của sơ đồ ở giai đoạn hai.

• Đánh giá mô hình cấu trúc.

Bên cạnh đó, các phân tích bổ sung như xác định chỉ số dự báo Q2 thông qua kỹ thuật Blindfolding hoặc phân tích bản đồ IPMA sẽ được thực hiện dựa trên sơ đồ của giai đoạn hai.

4. Thực hành xử lý biến bậc hai trong SMARTPLS 3

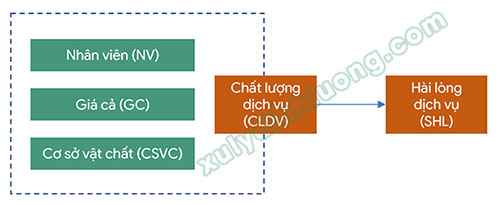
Xem xét một mô hình nghiên cứu với cấu trúc biến như sau.

– Biến Chất lượng dịch vụ được xây dựng là biến bậc hai theo hướng kết quả – nguyên nhân, được hình thành từ ba biến bậc một gồm Nhân viên với bốn biến quan sát, Giá cả với ba biến quan sát và Cơ sở vật chất với bốn biến quan sát.

– Biến Hài lòng dịch vụ là biến bậc một, được đo lường thông qua bốn biến quan sát theo hướng kết quả.

Nghiên cứu sử dụng bộ dữ liệu khảo sát với cỡ mẫu 150, phù hợp với cấu trúc mô hình đề xuất. Dữ liệu được nhập và phân tích bằng phần mềm SMARTPLS.

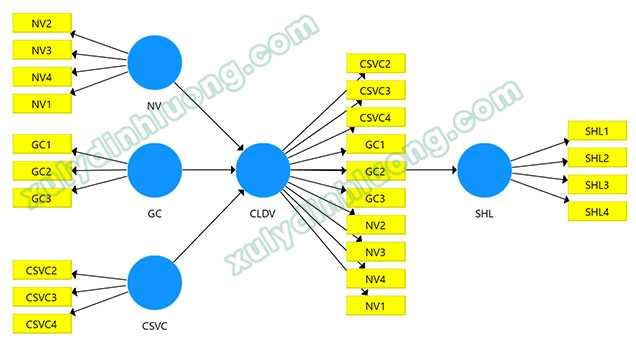
Bước 1: Biểu diễn mô hình nghiên cứu lý thuyết trên sơ đồ SMARTPLS theo phương pháp biến quan sát lặp lại.

Mối quan hệ giữa biến bậc hai và các biến bậc một được xác định theo hướng nguyên nhân, do đó cần thiết lập mũi tên từ các biến bậc một hướng lên biến bậc hai. Với cách tiếp cận biến quan sát lặp lại, toàn bộ các biến quan sát thuộc Nhân viên, Giá cả và Cơ sở vật chất được gán đồng thời cho biến Chất lượng dịch vụ. Hướng mũi tên giữa biến bậc hai và các biến quan sát được gán phải nhất quán với hướng mối quan hệ giữa biến bậc một và các biến quan sát. Cụ thể, nếu biến bậc một được đo lường theo dạng thang đo kết quả thì biến bậc hai với các biến quan sát lặp lại cũng phải được thiết lập theo dạng thang đo kết quả.

Bước 2: Đánh giá mô hình đo lường của các biến bậc một.

Tùy thuộc vào việc biến bậc một được mô hình hóa theo hướng kết quả hay nguyên nhân, tiêu chí đánh giá mô hình đo lường sẽ có sự khác biệt. Trong trường hợp này, các biến bậc một đều là biến kết quả, do đó việc đánh giá tập trung vào chất lượng biến quan sát, độ tin cậy thang đo, giá trị hội tụ và giá trị phân biệt. Phân tích được thực hiện thông qua thuật toán PLS Algorithm để thu thập các bảng kết quả cần thiết.

1. Đánh giá chất lượng biến quan sát

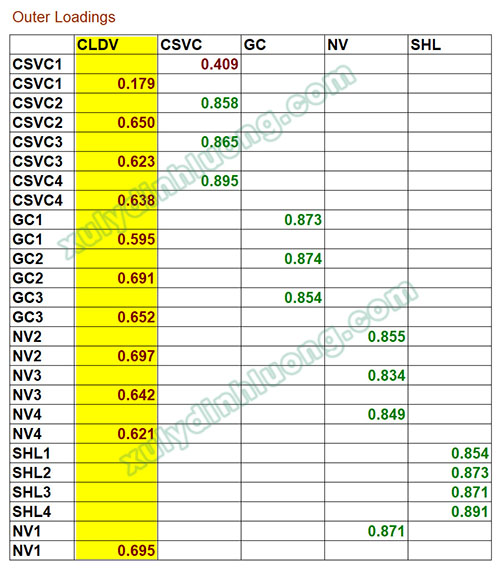
Trong bước này, các biến quan sát của biến bậc hai không được xem xét. Do đó, cột tương ứng với biến Chất lượng dịch vụ và các dòng biến quan sát liên quan đến biến này được loại bỏ khỏi bảng kết quả. Bảng hệ số tải ngoài được trình bày lại trên cơ sở các biến bậc một.

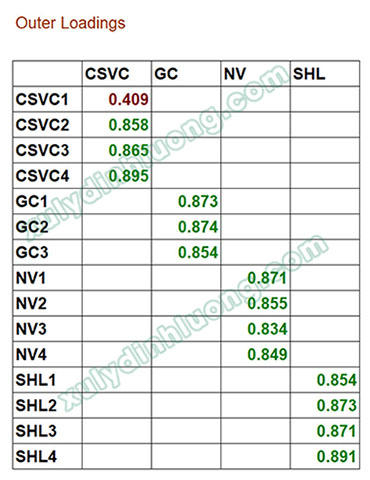
→ Kết quả cho thấy biến quan sát CSVC1 có hệ số tải ngoài bằng 0.409, thấp hơn ngưỡng chấp nhận 0.7, nên biến này không đạt yêu cầu và cần được loại khỏi mô hình. Nghiên cứu quay lại sơ đồ SMARTPLS, sao chép sơ đồ hiện tại và đặt tên mới để phân biệt với sơ đồ ban đầu, sau đó loại bỏ biến CSVC1 khỏi nhóm Cơ sở vật chất, đồng thời xóa biến này khỏi tập biến quan sát của Chất lượng dịch vụ.

Cần lưu ý rằng mỗi lần loại bỏ biến quan sát hoặc điều chỉnh cấu trúc mô hình, nghiên cứu đều tạo một sơ đồ mới thay vì chỉnh sửa trực tiếp trên sơ đồ cũ. Cách tiếp cận này nhằm đảm bảo khả năng theo dõi và trình bày đầy đủ các bước điều chỉnh mô hình trong phần phụ lục của nghiên cứu.

Sau khi loại bỏ biến CSVC1, thuật toán PLS Algorithm được chạy lại và bảng hệ số tải ngoài được kiểm tra lần nữa để đánh giá lại chất lượng các biến quan sát.

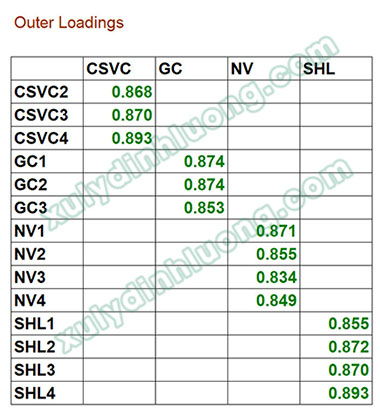
→ Kết quả phân tích cho thấy tất cả các biến quan sát còn lại đều có hệ số tải ngoài lớn hơn 0.7, chứng tỏ các biến quan sát này đạt yêu cầu và có ý nghĩa trong mô hình nghiên cứu.

2. Độ tin cậy và giá trị hội tụ của thang đo

Nghiên cứu tiến hành đánh giá độ tin cậy và giá trị hội tụ của các thang đo ở cấp độ biến tiềm ẩn bậc một (LOC), chưa xem xét biến tiềm ẩn bậc hai (HOC) ở giai đoạn này.

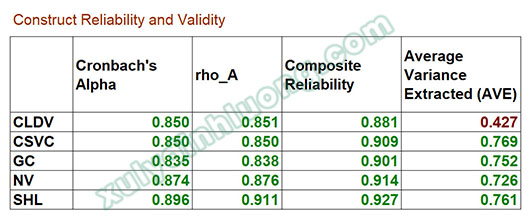
→ Trong quá trình xử lý biến bậc hai bằng phần mềm SmartPLS, kết quả cho thấy hệ số Cronbach’s Alpha và Composite Reliability của tất cả các LOC đều lớn hơn 0,7. Điều này cho thấy các thang đo LOC đạt mức độ tin cậy cao và đáp ứng yêu cầu về độ nhất quán nội tại.

→ Bên cạnh đó, giá trị phương sai trích trung bình (AVE) của các LOC đều lớn hơn 0,5, phản ánh các thang đo này đảm bảo giá trị hội tụ. Đối với AVE của biến bậc hai CLDV, cần lưu ý rằng SmartPLS tính toán chỉ số này dựa trên các biến quan sát được kéo trực tiếp vào CLDV, thay vì dựa trên các LOC. Tuy nhiên, theo cơ sở lý thuyết đã trình bày ở phần trước, việc đánh giá mô hình đo lường của HOC tập trung vào mối quan hệ giữa HOC và các LOC, chứ không phải mối quan hệ giữa HOC và các biến quan sát. Do đó, chỉ số AVE của biến CLDV không được sử dụng trong nghiên cứu này. Khi trình bày kết quả trong bài nghiên cứu, có thể loại bỏ hàng kết quả tương ứng với biến CLDV.

3. Giá trị phân biệt của thang đo

Giá trị phân biệt của các thang đo được đánh giá ở cấp độ LOC thông qua tiêu chí Fornell–Larcker và chỉ số HTMT, không thực hiện đánh giá đối với biến bậc hai HOC. Trong ví dụ minh họa, bảng HTMT được sử dụng làm mẫu; việc nhận xét đối với bảng Fornell–Larcker được thực hiện tương tự.

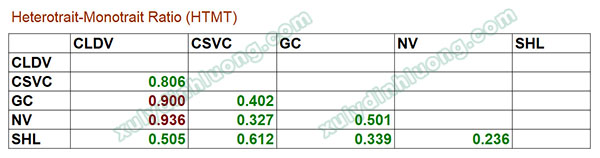
Trong quá trình xử lý biến bậc hai bằng SmartPLS, khi đọc kết quả và trình bày trong bài nghiên cứu, các giá trị thuộc hàng và cột của biến CLDV cần được bỏ qua. Có thể loại bỏ hoàn toàn hàng và cột CLDV, chỉ giữ lại bảng kết quả của các LOC.

→ Kết quả cho thấy giữa các cặp biến LOC, giá trị HTMT đều nhỏ hơn 0,85, qua đó khẳng định giá trị phân biệt giữa các thang đo LOC được đảm bảo.