Phân tích tương quan Pearson là một bước quan trọng trong quy trình nghiên cứu định lượng sử dụng phần mềm SPSS, thường được thực hiện trước khi tiến hành phân tích hồi quy. Bước phân tích này giúp nhà nghiên cứu đánh giá mối liên hệ ban đầu giữa các biến trong mô hình nghiên cứu.
Phân tích tương quan Pearson trong SPSS được sử dụng nhằm kiểm định mức độ và chiều hướng của mối quan hệ tuyến tính giữa biến phụ thuộc và các biến độc lập, đồng thời hỗ trợ phát hiện sớm hiện tượng đa cộng tuyến trong trường hợp các biến độc lập có mối tương quan mạnh với nhau.
VIDEO
1. Cơ sở lý thuyết về tương quan Pearson
Tương quan tuyến tính giữa hai biến được hiểu là mối quan hệ mà khi biểu diễn các giá trị quan sát của hai biến trên hệ trục tọa độ Oxy, các điểm dữ liệu có xu hướng phân bố gần một đường thẳng. Theo Gayen (1951), trong thống kê, hệ số tương quan Pearson (ký hiệu là r) được sử dụng để đo lường mức độ chặt chẽ của mối quan hệ tuyến tính giữa hai biến định lượng. Trong trường hợp một hoặc cả hai biến không thuộc loại biến định lượng, chẳng hạn như biến định tính hoặc biến nhị phân, phân tích tương quan Pearson sẽ không được áp dụng.
Hệ số tương quan Pearson r có giá trị nằm trong khoảng từ -1 đến 1.
- Khi giá trị r tiến gần về 1 hoặc -1, mối tương quan tuyến tính giữa hai biến càng mạnh; r tiến về 1 phản ánh mối tương quan dương, trong khi r tiến về -1 thể hiện mối tương quan âm.
- Ngược lại, khi r tiến gần về 0, mức độ tương quan tuyến tính giữa hai biến càng yếu.
- Trường hợp r bằng 1 cho thấy tồn tại mối tương quan tuyến tính hoàn hảo, khi đó các điểm dữ liệu trên đồ thị phân tán sẽ nằm trên cùng một đường thẳng.
- Nếu r bằng 0, không tồn tại mối tương quan tuyến tính giữa hai biến; điều này có thể xuất phát từ việc hai biến hoàn toàn không có mối liên hệ hoặc tồn tại mối quan hệ phi tuyến.
Theo Andy Field (2009), bên cạnh việc xác định hệ số tương quan Pearson, cần tiến hành kiểm định giả thuyết để đánh giá ý nghĩa thống kê của hệ số này. Nếu giá trị sig của kiểm định nhỏ hơn 0.05, có thể kết luận rằng giữa hai biến tồn tại mối tương quan tuyến tính có ý nghĩa thống kê; ngược lại, nếu sig lớn hơn 0.05, không đủ cơ sở để khẳng định mối tương quan tuyến tính giữa hai biến, với mức ý nghĩa được sử dụng là 5%.
Sau khi xác nhận mối tương quan tuyến tính có ý nghĩa thống kê, mức độ mạnh hay yếu của mối quan hệ sẽ được đánh giá dựa trên giá trị tuyệt đối của hệ số r. Cụ thể, theo phân loại của Andy Field (2009),
- Nếu |r| nhỏ hơn 0.1 thì mối tương quan được xem là rất yếu;
- |r| nhỏ hơn 0.3 phản ánh mối tương quan yếu;
- |r| nhỏ hơn 0.5 cho thấy mối tương quan ở mức trung bình;
- Và khi |r| lớn hơn hoặc bằng 0.5, mối tương quan được đánh giá là mạnh.
2. Phân tích tương quan Pearson bằng phần mềm SPSS 26
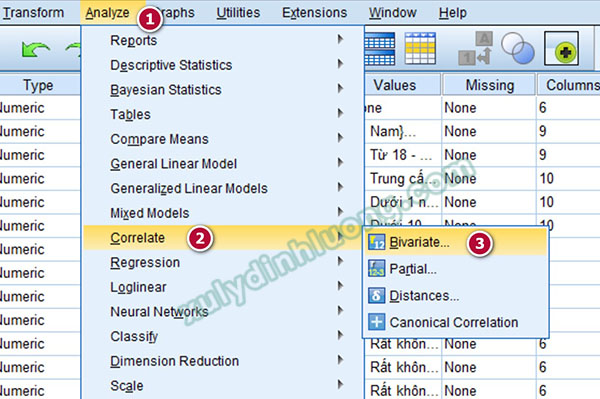
Phân tích tương quan được sử dụng nhằm đánh giá mức độ và chiều hướng mối quan hệ tuyến tính giữa các biến nghiên cứu. Trong SPSS 26, thao tác được thực hiện thông qua đường dẫn Analyze > Correlate > Bivariate.
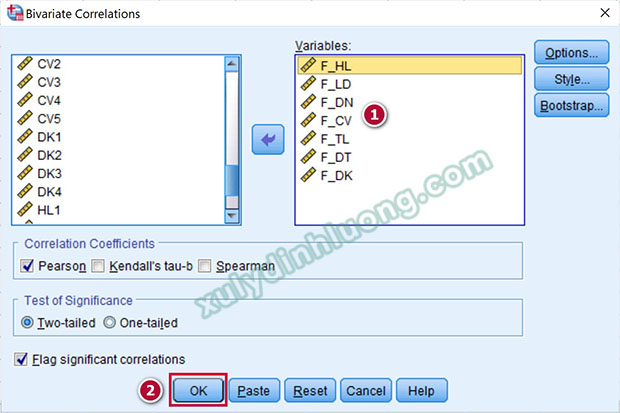
Tại hộp thoại Bivariate Correlations, toàn bộ các biến cần phân tích tương quan Pearson được đưa vào mục Variables. Để thuận tiện cho việc quan sát và diễn giải kết quả, biến phụ thuộc nên được sắp xếp ở vị trí đầu tiên. Trong ví dụ minh họa, biến F_HL được xác định là biến phụ thuộc, các biến còn lại đóng vai trò là biến độc lập. Sau khi hoàn tất việc lựa chọn biến, người nghiên cứu nhấn OK để thực hiện phân tích.
Kết quả phân tích tương quan Pearson được trình bày trong bảng Correlations. Trong bảng này, Pearson Correlation thể hiện hệ số tương quan Pearson (r), phản ánh mức độ và chiều hướng mối quan hệ giữa hai biến. Sig. (2-tailed) là giá trị xác suất của kiểm định t, dùng để đánh giá ý nghĩa thống kê của hệ số tương quan Pearson. N biểu thị kích thước mẫu được sử dụng trong phân tích.
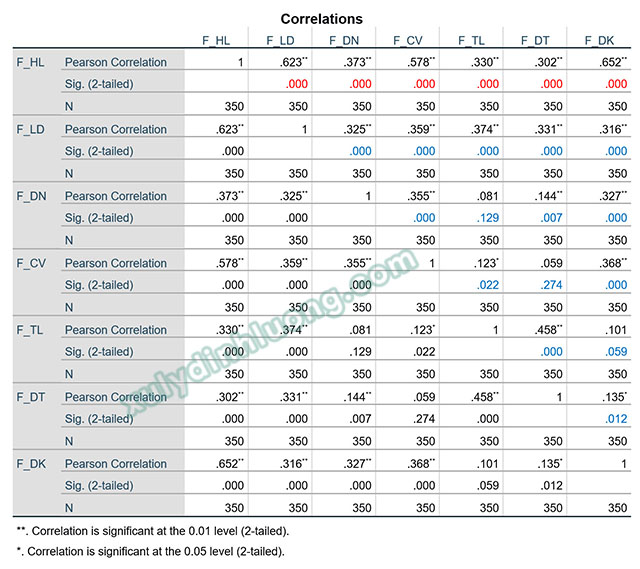
3. Đọc và diễn giải kết quả tương quan Pearson
Khi phân tích kết quả, cần xem xét hai nhóm mối quan hệ tương quan chính: mối quan hệ giữa biến phụ thuộc với các biến độc lập và mối quan hệ tương quan giữa các biến độc lập với nhau. Việc phân tách này là cần thiết do kỳ vọng và mục đích đánh giá đối với từng loại mối quan hệ có sự khác biệt nhất định trong nghiên cứu định lượng.
3.1 Mối quan hệ giữa biến độc lập và biến phụ thuộc
Bảng kết quả trình bày phía trên thể hiện các giá trị sig được đánh dấu bằng màu đỏ. Trong quá trình xây dựng mô hình nghiên cứu, các biến độc lập đã được lựa chọn thông qua việc xem xét cẩn trọng cơ sở lý thuyết, tổng hợp các nghiên cứu trước có liên quan và đánh giá điều kiện thực tiễn tại bối cảnh khảo sát. Trên cơ sở đó, nghiên cứu kỳ vọng rằng kết quả phân tích dữ liệu sẽ phản ánh sự tồn tại của mối quan hệ giữa các biến độc lập và biến phụ thuộc. Khi tiến hành phân tích tương quan trước bước hồi quy, nếu kết quả tương quan Pearson cho thấy biến độc lập có mối liên hệ với biến phụ thuộc thì khả năng biến đó có tác động đến biến phụ thuộc trong mô hình hồi quy là tương đối cao.
Cụ thể, trong bảng kết quả minh họa, giá trị sig của kiểm định tương quan Pearson giữa sáu biến độc lập gồm F_LD, F_DN, F_CV, F_TL, F_DT, F_DK và biến phụ thuộc F_HL đều nhỏ hơn 0.05. Điều này cho thấy tồn tại mối quan hệ tuyến tính có ý nghĩa thống kê giữa các biến độc lập này với biến phụ thuộc.
Kỳ vọng đặt ra là giá trị sig của hệ số tương quan giữa biến độc lập và biến phụ thuộc nhỏ hơn 0.05, đồng thời hệ số tương quan đạt giá trị càng lớn thì mức độ liên hệ càng mạnh.
3.2 Mối quan hệ giữa các biến độc lập
Trong bảng kết quả tương quan, các giá trị sig được thể hiện bằng màu xanh dương. Khái niệm “biến độc lập” phản ánh kỳ vọng rằng các biến này có ý nghĩa riêng biệt và không phụ thuộc lẫn nhau. Trường hợp hai biến độc lập có mức độ tương quan quá cao, có thể cho thấy chúng phản ánh cùng một khái niệm tiềm ẩn. Khi hai biến độc lập không có tương quan với nhau, thể hiện qua giá trị sig lớn hơn 0.05, khả năng xảy ra hiện tượng đa cộng tuyến là rất thấp. Ngược lại, nếu hai biến độc lập có tương quan với sig nhỏ hơn 0.05 và trị tuyệt đối của hệ số tương quan lớn hơn 0.7, thì nguy cơ xảy ra đa cộng tuyến giữa hai biến là tương đối cao (Carsten F. Dormann và cộng sự, 2013).
Tuy nhiên, việc đánh giá đa cộng tuyến không nên chỉ dựa trên hệ số tương quan Pearson mà cần được kết hợp với chỉ số VIF trong phân tích hồi quy tuyến tính nhằm đưa ra kết luận chính xác hơn. Chỉ số VIF thường được sử dụng như một tiêu chí bổ sung để xác định mức độ ảnh hưởng của đa cộng tuyến trong mô hình.
Kỳ vọng của nghiên cứu là hệ số tương quan giữa các biến độc lập có giá trị nhỏ hơn 0.7.
Ý nghĩa hai dòng cuối trong kết quả phân tích Pearson
Khi giá trị sig nhỏ hơn 0.05, tại vị trí hệ số tương quan Pearson sẽ xuất hiện ký hiệu * hoặc **.
- Ký hiệu ** cho biết cặp biến có mối tương quan tuyến tính với mức độ tin cậy 99%, tương ứng với mức ý nghĩa 1% (0.01).
- Ký hiệu * cho biết cặp biến có mối tương quan tuyến tính với mức độ tin cậy 95%, tương ứng với mức ý nghĩa 5% (0.05).