Trong lĩnh vực PLS-SEM, nhiều phương pháp đã được các học giả đề xuất nhằm xác định và ước lượng các khái niệm bậc hai. Trong số đó, hai phương pháp được sử dụng phổ biến nhất bao gồm phương pháp chỉ báo lặp lại (hoặc chỉ báo lặp lại mở rộng) và phương pháp hai giai đoạn (Ringle và cộng sự, 2012).
Trước khi trình bày chi tiết nội dung nghiên cứu, cần làm rõ một số thuật ngữ và ký hiệu liên quan đến mô hình khái niệm bậc cao như sau:
HOC (higher-order component hoặc higher-order construct) được sử dụng để chỉ khái niệm bậc hai, trong đó bao hàm các khái niệm bậc một.
LOC (lower-order component hoặc lower-order construct) dùng để chỉ các khái niệm bậc một cấu thành nên một khái niệm bậc hai.
Repeated Indicators Approach là phương pháp tiếp cận chỉ báo lặp lại, trong đó các biến quan sát của khái niệm bậc một được sử dụng đồng thời để đo lường khái niệm bậc hai.
Two-Stage Approach là phương pháp tiếp cận hai giai đoạn trong ước lượng mô hình.
Formative đề cập đến thang đo dạng nguyên nhân.
Reflective đề cập đến thang đo dạng kết quả.
Thuật ngữ biến bậc hai nguyên nhân hoặc biến bậc hai formative được sử dụng khi mối quan hệ giữa biến bậc hai và các biến bậc một thành phần là quan hệ nguyên nhân. Trong trường hợp này, mối quan hệ giữa các biến bậc một và các biến quan sát tương ứng có thể là dạng kết quả hoặc nguyên nhân.
Ngược lại, biến bậc hai kết quả hoặc biến bậc hai reflective được hiểu là trường hợp mối quan hệ giữa biến bậc hai và các biến bậc một thành phần là quan hệ kết quả. Khi đó, mối quan hệ giữa các biến bậc một và các biến quan sát của chúng không bị giới hạn ở một dạng đo lường cụ thể, có thể là reflective hoặc formative.
1. So sánh phương pháp chỉ báo lặp lại và phương pháp hai giai đoạn
Theo Becker và cộng sự (2012), khi kích thước mẫu đủ lớn, phương pháp chỉ báo lặp lại và phương pháp hai giai đoạn thường mang lại kết quả ước lượng tương đối tương đồng. Phương pháp chỉ báo lặp lại được đánh giá là dễ triển khai trong PLS-SEM; tuy nhiên, phương pháp này bộc lộ nhiều hạn chế khi áp dụng cho các biến bậc hai có cấu trúc nguyên nhân. Do đó, phương pháp hai giai đoạn đã được đề xuất như một giải pháp thay thế phù hợp hơn trong những trường hợp này (Wetzels và cộng sự, 2009).
Nghiên cứu của Ringle và cộng sự (2019) cho thấy số lượng các công trình khoa học áp dụng phương pháp hai giai đoạn trong việc xử lý các khái niệm bậc hai chiếm tỷ lệ cao hơn đáng kể so với phương pháp chỉ báo lặp lại, phản ánh xu hướng ưu tiên phương pháp này trong nghiên cứu thực nghiệm hiện nay.
Dưới đây là bảng so sánh nhanh về ứng dụng của kỹ thuật xử lý biến bậc hai này:
| Tiêu chí | Repeated Indicators Approach | Two-Stage Approach |
| 1. Nguyên lý | Phương pháp này sử dụng toàn bộ các chỉ báo quan sát của các biến tiềm ẩn bậc một làm chỉ báo trực tiếp cho biến tiềm ẩn bậc hai, qua đó ước lượng đồng thời các cấp độ trong cùng một mô hình. | Phương pháp được triển khai theo hai giai đoạn tách biệt. Giai đoạn thứ nhất ước lượng các biến tiềm ẩn bậc một và trích xuất điểm số biến tiềm ẩn. Giai đoạn thứ hai sử dụng các điểm số này như các chỉ báo đầu vào để ước lượng biến tiềm ẩn bậc hai. |
| 2. Công việc thực hiện | Quy trình thiết lập tương đối đơn giản, dễ áp dụng trong thực nghiệm và không đòi hỏi nhiều bước xử lý hay thao tác kỹ thuật phức tạp. | Quy trình thực hiện phức tạp hơn do phải tiến hành phân tích qua hai mô hình riêng biệt, đòi hỏi người nghiên cứu có hiểu biết rõ ràng về trình tự và kỹ thuật phân tích. |
| 3. Phạm vi ứng dụng | Phương pháp này chủ yếu phù hợp với các mô hình biến bậc hai có dạng phản xạ, trong đó biến bậc hai được xem là kết quả của các biến bậc một. | Phương pháp có khả năng xử lý hiệu quả cả biến bậc hai dạng phản xạ lẫn dạng hình thành, cho phép linh hoạt hơn trong thiết kế mô hình nghiên cứu. |
| 4. Quan hệ của biến bậc một với bậc hai | Không cho phép đánh giá trực tiếp mối quan hệ riêng biệt giữa từng biến bậc một và biến bậc hai do các chỉ báo được lặp lại trong cùng một cấu trúc mô hình. | Cho phép đánh giá rõ ràng mối quan hệ giữa các biến bậc một và biến bậc hai thông qua các hệ số ước lượng ở giai đoạn thứ hai. |
| 5. Đọc kết quả | Việc diễn giải kết quả tương đối thuận tiện do toàn bộ quá trình phân tích được thực hiện trong một mô hình duy nhất. | Việc diễn giải kết quả phức tạp hơn nhưng toàn diện hơn, do cần tổng hợp và so sánh kết quả thu được từ hai mô hình tương ứng với hai giai đoạn phân tích. |
2. Chức năng của từng giai đoạn trong phương pháp hai giai đoạn
Phương pháp xử lý biến bậc hai theo cách tiếp cận hai giai đoạn (Two-Stage Approach) trong mô hình PLS-SEM được triển khai thông qua hai bước tách biệt, trong đó mỗi giai đoạn đảm nhận một vai trò cụ thể trong quá trình ước lượng và đánh giá mô hình. Nội dung dưới đây trình bày chi tiết chức năng của từng giai đoạn.
Giai đoạn 1: Ước lượng các cấu trúc bậc một (Lower-Order Constructs – LOCs)
Mục tiêu trọng tâm của giai đoạn thứ nhất là ước lượng các biến tiềm ẩn bậc một và thu thập điểm số biến tiềm ẩn của các cấu trúc này nhằm phục vụ cho việc xây dựng biến bậc hai ở giai đoạn tiếp theo.
a. Đánh giá chất lượng mô hình đo lường của các LOCs
Trước hết, cần tiến hành kiểm định độ tin cậy của thang đo nhằm đánh giá mức độ nhất quán nội bộ của từng cấu trúc bậc một. Việc này thường được thực hiện thông qua các chỉ số như Cronbach’s Alpha và Composite Reliability.
Tiếp theo, giá trị hội tụ của thang đo được xem xét để đảm bảo rằng các biến quan sát phản ánh cùng một cấu trúc tiềm ẩn có mức độ tương quan đủ lớn. Chỉ số Average Variance Extracted thường được sử dụng cho mục đích này.
Giá trị phân biệt cũng cần được kiểm định nhằm xác nhận rằng mỗi cấu trúc bậc một thể hiện một khái niệm riêng biệt và không trùng lặp với các cấu trúc khác trong mô hình. Các tiêu chí phổ biến bao gồm Fornell-Larcker và tỷ lệ HTMT.
Đối với các LOCs được đo lường theo dạng formative, vấn đề cộng tuyến giữa các biến quan sát cần được kiểm tra thông qua chỉ số Variance Inflation Factor để đảm bảo không tồn tại hiện tượng đa cộng tuyến ở mức nghiêm trọng.
b. Trích xuất điểm số biến tiềm ẩn của các LOCs
Sau khi mô hình đo lường của các cấu trúc bậc một được xác nhận đạt yêu cầu về độ tin cậy và giá trị, phần mềm PLS-SEM sẽ tạo ra điểm số biến tiềm ẩn cho từng LOC. Các điểm số này phản ánh giá trị tổng hợp của mỗi cấu trúc bậc một và được sử dụng làm dữ liệu đầu vào cho giai đoạn tiếp theo.
Giai đoạn 2: Mô hình hóa cấu trúc bậc hai (Higher-Order Construct – HOC)
Giai đoạn thứ hai tập trung vào việc sử dụng điểm số biến tiềm ẩn của các LOCs thu được từ giai đoạn một để đại diện cho cấu trúc bậc hai và tiến hành đánh giá các mối quan hệ trong mô hình cấu trúc.
a. Thiết lập mô hình mới với biến bậc hai
Trong giai đoạn này, các điểm số biến tiềm ẩn của các cấu trúc bậc một được sử dụng như các biến quan sát nhằm đo lường cấu trúc bậc hai. Mô hình cấu trúc được xây dựng lại để phản ánh vai trò của HOC và các mối liên hệ giữa HOC với các biến khác trong mô hình, bao gồm biến độc lập, biến phụ thuộc, cũng như các biến trung gian hoặc điều tiết nếu có.
b. Đánh giá mô hình đo lường của HOC
Trường hợp cấu trúc bậc hai được mô hình hóa theo hướng phản xạ, cần xem xét mức độ đóng góp và ý nghĩa giải thích của các cấu trúc bậc một đối với HOC, đồng thời kiểm tra chỉ số VIF giữa các LOCs để đảm bảo không xảy ra hiện tượng cộng tuyến.
Trong trường hợp HOC được hình thành theo hướng formative, việc kiểm tra VIF giữa các cấu trúc bậc một đóng vai trò là chỉ số đo lường của HOC là yêu cầu bắt buộc nhằm loại trừ nguy cơ đa cộng tuyến.
c. Đánh giá mô hình cấu trúc
Cuối cùng, mô hình cấu trúc được đánh giá thông qua việc kiểm định ý nghĩa thống kê của các mối quan hệ nhân quả. Các hệ số đường dẫn giữa HOC và các biến khác được kiểm tra bằng kỹ thuật Bootstrap để xác định giá trị t và mức ý nghĩa thống kê.
Bên cạnh đó, các chỉ số R-squared và Q-squared được sử dụng để đánh giá khả năng giải thích và năng lực dự báo của mô hình. Mức độ ảnh hưởng của HOC đối với biến phụ thuộc được xác định thông qua chỉ số f-squared nhằm làm rõ vai trò tương đối của cấu trúc bậc hai trong mô hình nghiên cứu.
Mặc dù PLS-SEM không đặt trọng tâm vào các chỉ số độ phù hợp mô hình như trong CB-SEM, một số chỉ số tổng quát như SRMR vẫn có thể được sử dụng để xem xét mức độ phù hợp tổng thể của mô hình.
3. Các phiên bản của phương pháp hai giai đoạn
Ưu điểm nổi bật của phương pháp tiếp cận hai giai đoạn là khả năng áp dụng cho mọi dạng mô hình bậc cao. Do đó, trong thực hành nghiên cứu, kỹ thuật này thường được ưu tiên khi xử lý các mô hình có chứa biến bậc hai, bất kể biến bậc hai đóng vai trò là biến phụ thuộc hay biến độc lập. Trong khuôn khổ bài viết này, tác giả tập trung trình bày và hướng dẫn cách xử lý mô hình bậc cao thông qua phương pháp hai giai đoạn.
Trong tài liệu học thuật, hai phiên bản của phương pháp hai giai đoạn đã được đề xuất, bao gồm:
(1) phương pháp hai giai đoạn nhúng (embedded two-stage approach) do Ringle và cộng sự (2012) giới thiệu, và
(2) phương pháp hai giai đoạn tách biệt (disjoint two-stage approach) được đề cập trong các nghiên cứu của Agarwal và Karahanna (2000) cũng như Becker và cộng sự (2012).
Hai phiên bản này có một số khác biệt nhất định trong cách thiết lập mô hình ở từng giai đoạn phân tích.
Cụ thể, phương pháp nhúng tiến hành mô hình hóa toàn bộ khái niệm bậc hai ngay từ giai đoạn đầu, trong khi phương pháp tách biệt chỉ sử dụng các cấu trúc bậc thấp ở giai đoạn ban đầu, qua đó phản ánh đúng bản chất “nhúng” và “tách biệt” của hai cách tiếp cận. Tuy nhiên, các bằng chứng thực nghiệm cho thấy hai phiên bản của phương pháp hai giai đoạn thường tạo ra kết quả ước lượng tương đương nhau (Cheah và cộng sự, 2019). Vì vậy, hiện chưa có cơ sở lý thuyết hoặc thực nghiệm rõ ràng để khẳng định ưu thế tuyệt đối của một phương pháp so với phương pháp còn lại.
2.1. Phương pháp hai giai đoạn nhúng (embedded two-stage approach)
Giai đoạn 1 (Stage 1)
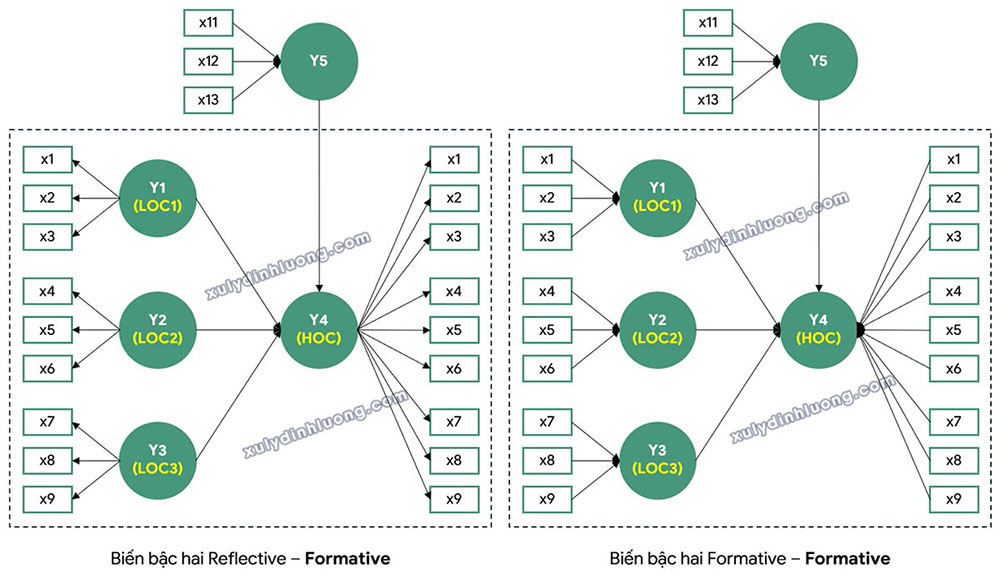
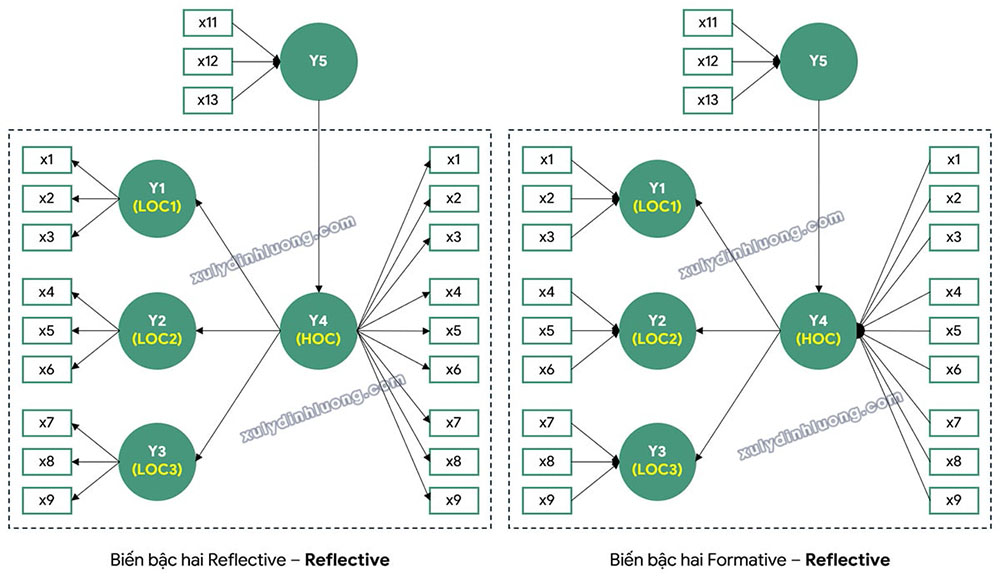
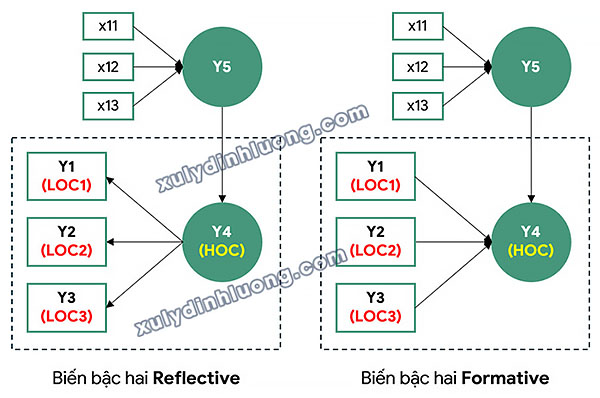
Xét mô hình nghiên cứu minh họa trong Hình 1 và Hình 2. Trong mô hình này, Y5 là biến bậc một, trong khi Y4 là biến bậc hai (higher-order construct) được cấu thành từ ba biến bậc một thành phần Y1, Y2 và Y3 (lower-order constructs).
Giai đoạn 1 của phương pháp hai giai đoạn nhúng về mặt kỹ thuật tương tự với phương pháp chỉ báo lặp lại. Theo đó, toàn bộ các biến quan sát của các biến bậc một được gán đồng thời cho biến bậc hai. Điều này dẫn đến việc mỗi biến quan sát được sử dụng hai lần trong mô hình: một lần để đo lường biến bậc một tương ứng và một lần nữa để khai báo cho biến bậc hai (các chỉ báo x1 đến x9 trong Hình 1 và Hình 2).
Một số điểm cần lưu ý trong quá trình thiết lập mô hình ở giai đoạn này bao gồm:
- Thứ nhất, các biến quan sát của biến bậc một khi được gán cho biến bậc hai chỉ đóng vai trò khai báo và nhận diện biến bậc hai trên phần mềm phân tích, chứ không phản ánh thang đo đo lường thực sự của biến bậc hai.
- Thứ hai, việc đo lường khái niệm bậc hai về bản chất được xác định thông qua mối quan hệ cấu trúc giữa biến bậc hai và các biến bậc một thành phần.
- Thứ ba, trong trường hợp một biến quan sát của biến bậc một bị loại bỏ do không đáp ứng các tiêu chuẩn kiểm định, biến quan sát đó cần được loại bỏ đồng thời khỏi cả cấu trúc bậc một và cấu trúc bậc hai.
Đối với các nhân tố còn lại trong mô hình (chẳng hạn Y5 trong Hình 3), việc đo lường được thực hiện thông qua một biến đơn với một chỉ báo duy nhất. Chỉ báo này chính là điểm số biến tiềm ẩn của nhân tố tương ứng thu được từ giai đoạn 1.
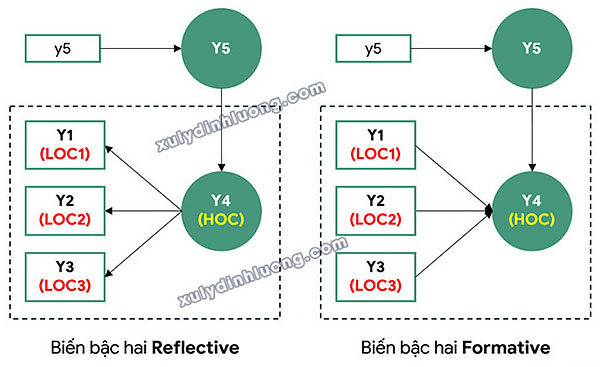
Trong ví dụ minh họa ở Hình 1 và Hình 2, cấu trúc bậc hai Y4 ở giai đoạn 2 được đo lường bằng ba chỉ báo hình thành, đại diện cho điểm số biến tiềm ẩn của ba biến bậc một Y1, Y2 và Y3 được ước lượng trong giai đoạn trước.
2.2. Phương pháp hai giai đoạn tách biệt (disjoint two-stage approach)
Phương pháp hai giai đoạn tách biệt khác với phương pháp nhúng ở cách thức xây dựng và ước lượng mô hình tại từng giai đoạn phân tích.
Giai đoạn 1 (Stage 1)
Trong giai đoạn thứ nhất, phương pháp hai giai đoạn tách biệt không áp dụng kỹ thuật chỉ báo lặp lại. Thay vào đó, mô hình đường dẫn chỉ bao gồm các biến tiềm ẩn bậc một cấu thành nên biến tiềm ẩn bậc hai, và không xuất hiện đồng thời biến bậc hai trong mô hình. Các biến bậc một này được kết nối trực tiếp với toàn bộ các biến khác trong mô hình theo các mối quan hệ lý thuyết mà biến bậc hai đại diện. Cách tiếp cận này cho phép ước lượng các mối quan hệ giữa các biến bậc một và các khái niệm liên quan mà không chịu ảnh hưởng trực tiếp từ cấu trúc bậc hai.
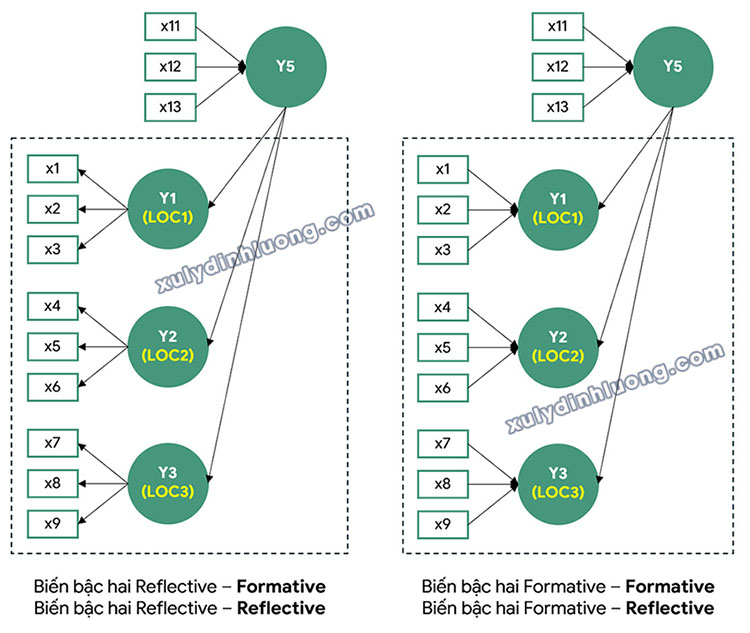
Giai đoạn 2 (Stage 2)
Sau khi hoàn tất việc ước lượng mô hình ở giai đoạn 1, các điểm số của biến tiềm ẩn được trích xuất và lưu lại, nhưng chỉ đối với các biến tiềm ẩn bậc một thành phần (ví dụ như điểm số của các nhân tố Y1, Y2 và Y3 trong mô hình minh họa). Sang giai đoạn thứ hai, các điểm số này được sử dụng làm chỉ báo trong mô hình đo lường của khái niệm bậc hai, như được trình bày trong Hình 6.
Khác với phương pháp nhúng, các biến tiềm ẩn còn lại trong mô hình đường dẫn ở giai đoạn hai vẫn được giữ nguyên cấu trúc đo lường ban đầu với các biến quan sát gốc, thay vì được chuyển đổi thành biến đơn với một chỉ báo duy nhất. Chẳng hạn, trong Hình 6, nhân tố Y5 vẫn được đo lường bằng ba biến quan sát như ở giai đoạn 1, trong khi nếu áp dụng phương pháp nhúng, nhân tố này sẽ được rút gọn thành một biến quan sát duy nhất.
———-
Nguồn tham khảo:
Sarstedt, M., Hair, J. F., Cheah, J.-H., Becker, J.-M., & Ringle, C. M. (2019). How to Specify, Estimate, and Validate Higher-Order Constructs in PLS-SEM. Australasian Marketing Journal, 27(3), 197-211.