Trong bài viết Phân tích CFA cấu trúc bậc hai (second order) trên AMOS, chúng ta đã làm rõ khái niệm biến bậc hai trong mô hình SEM, cách thức biểu diễn trên sơ đồ mô hình và quy trình thực hiện phân tích CFA. Tiếp nối nội dung đó, bài viết này tập trung trình bày phương pháp và các bước tiến hành phân tích SEM đối với biến bậc hai trên AMOS.
1. Biến bậc hai (second-order) và biến bậc một (first-order)
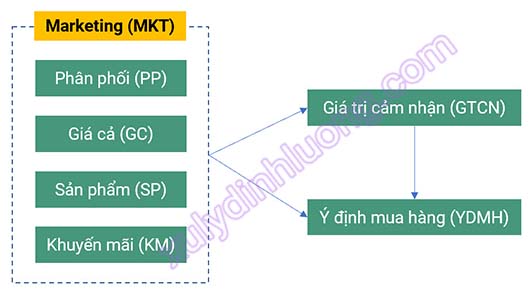
Trong trường hợp người đọc chưa nắm rõ khái niệm biến bậc hai, có thể tham khảo thêm tại bài viết này. Xét một cấu trúc biến bậc hai như sau: biến MKT (Marketing) được hình thành từ bốn biến bậc một, bao gồm PP (Phân phối), GC (Giá cả), SP (Sản phẩm) và KM (Khuyến mãi). Khi thể hiện trên mô hình lý thuyết, cấu trúc này có thể được minh họa dưới dạng sơ đồ mối quan hệ giữa biến bậc hai và các biến bậc một thành phần.
Thông tin về các biến trong mô hình được mô tả như sau:
-
MKT: Là biến bậc hai, không được đo lường trực tiếp bởi các biến quan sát. Biến bậc hai được ước lượng thông qua các biến bậc một cấu thành, do đó bản thân nó không có biến quan sát riêng.
-
PP: Là biến bậc một, được đo lường bởi hai biến quan sát và đóng vai trò là một thành phần của biến MKT.
-
GC: Là biến bậc một, bao gồm bốn biến quan sát và là một thành phần cấu thành của biến MKT.
-
SP: Là biến bậc một, gồm bốn biến quan sát và tham gia hình thành biến MKT.
-
KM: Là biến bậc một, được đo lường bởi hai biến quan sát và là một thành phần của biến MKT.
-
GTCN: Là biến bậc một, bao gồm ba biến quan sát.
-
YDMH: Là biến bậc một, được đo lường bởi bốn biến quan sát.
2. Biểu diễn biến bậc hai trong mô hình SEM bằng AMOS
Việc biểu diễn các biến trong mô hình lý thuyết được thực hiện trên sơ đồ SEM như sau:
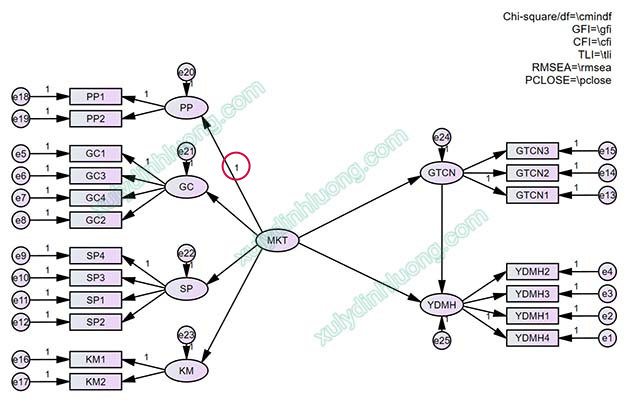
Các lưu ý khi xây dựng và biểu diễn biến bậc hai trong SEM AMOS bao gồm:
Thứ nhất, đối với các mũi tên đường dẫn từ biến bậc hai đến các biến bậc một thành phần, cần cố định một hệ số chặn bằng 1 tại mục Regression weight cho một trong các đường dẫn này nhằm đảm bảo điều kiện nhận dạng của mô hình.
Thứ hai, mỗi biến bậc một thành phần phải đi kèm với một biến sai số hay phần dư riêng. Trong minh họa nêu trên, bốn biến bậc một có bốn phần dư tương ứng, được ký hiệu lần lượt là e20 đến e23.
Thứ ba, các mũi tên hai chiều thể hiện mối tương quan hay hiệp phương sai giữa các biến tiềm ẩn độc lập phải được vẽ trực tiếp từ biến bậc hai đến các biến tiềm ẩn độc lập khác, thay vì nối từ các biến bậc một thành phần. Ví dụ, nếu bổ sung một biến tiềm ẩn độc lập NLPV gồm ba biến quan sát NLPV1, NLPV2 và NLPV3, có ảnh hưởng đến GTCN và YDMH, thì mối tương quan hai chiều sẽ được biểu diễn giữa NLPV và MKT.
Thứ tư, các mũi tên một chiều biểu diễn mối quan hệ nhân quả hoặc tác động chỉ được phép nối từ biến bậc hai đến các biến khác trong mô hình, không được xuất phát từ các biến bậc một thành phần. Trong ví dụ minh họa, chỉ xem xét tác động của MKT lên GTCN và YDMH, không xem xét tác động trực tiếp của các biến thành phần như PP, GC, SP hay KM lên các biến khác.
Trong trường hợp nghiên cứu mong muốn đánh giá trực tiếp ảnh hưởng của các biến bậc một thành phần lên các biến khác trong mô hình, cần xây dựng một sơ đồ SEM riêng biệt chỉ bao gồm các biến bậc một, không xuất hiện biến bậc hai, và tiến hành phân tích độc lập trên sơ đồ này. Việc sử dụng song song hai sơ đồ SEM, bao gồm một mô hình bậc một và một mô hình bậc hai, là cách tiếp cận phổ biến và được chấp nhận trong nghiên cứu sử dụng biến tiềm ẩn bậc hai.
3. Phân tích và diễn giải kết quả SEM với biến bậc hai
Việc tiến hành phân tích và diễn giải kết quả SEM trong mô hình có biến bậc hai về cơ bản không khác so với mô hình chỉ bao gồm các biến bậc một. Do đó, phần này không trình bày lại chi tiết quy trình đọc kết quả SEM, mà chỉ tập trung nhấn mạnh một số điểm cần lưu ý khi xử lý biến bậc hai. Trong mô hình nghiên cứu nêu trên, có ba mối quan hệ cấu trúc chính cần được xem xét, bao gồm: MKT → GTCN, MKT → YDMH và GTCN → YDMH.
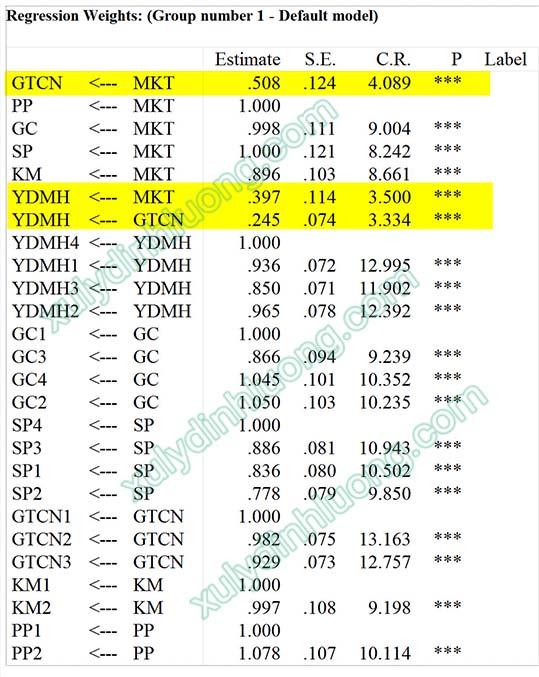
→ Kết quả cho thấy giá trị P-value của cả ba mối quan hệ đều bằng 0.000 và nhỏ hơn mức ý nghĩa 0.05, chứng tỏ các mối quan hệ này đều có ý nghĩa thống kê. Việc đánh giá mức độ và thứ tự tác động giữa các biến vẫn được thực hiện dựa trên bảng hệ số chuẩn hóa, tương tự như trong phân tích SEM thông thường.
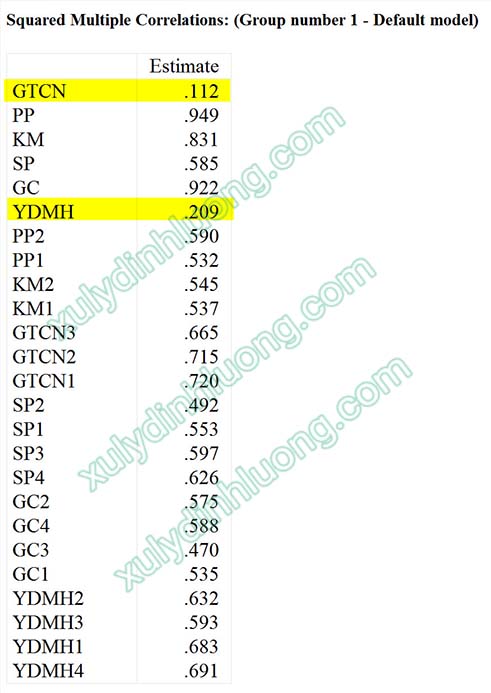
→ Trong mô hình nghiên cứu có hai biến đóng vai trò biến phụ thuộc là GTCN và YDMH, do đó chỉ cần xem xét hai giá trị R bình phương tương ứng trong bảng Squared Multiple Correlations để đánh giá mức độ giải thích của mô hình đối với các biến này.
Tóm lại, khi thực hiện phân tích SEM với biến bậc hai, việc đánh giá chủ yếu tập trung vào mối quan hệ giữa biến bậc hai và các biến khác trong mô hình cấu trúc. Trong bối cảnh này, biến bậc hai được xem xét và xử lý tương tự như một biến bậc một trong phân tích SEM thông thường.
