Một trong các chỉ số rất quan trọng mà chúng ta sẽ đọc kết quả ở bước phân tích hồi quy là giá trị R bình phương hiệu chỉnh. Vậy R bình phương hiệu chỉnh là gì? Ý nghĩa của chỉ số này ra sao? Chúng ta sẽ lần lượt đi vào từng chủ đề nội dung theo thứ tự bên dưới.
1. Hệ số R2 (R bình phương – R Square) là gì?
Các điểm dữ liệu luôn phân tán và có xu hướng tạo thành dạng một đường thẳng chứ không phải là một đường thẳng hoàn toàn. Do đó, hầu như không có đường thẳng nào có thể đi qua toàn bộ tất cả các điểm dữ liệu, luôn có sự sai lệch giữa các giá trị ước tính và các giá trị thực tế. Chúng ta sẽ cần tính toán được mức độ sai lệch đó cũng như mức độ phù hợp của mô hình hồi quy tuyến tính với tập dữ liệu. Một thước đo sự phù hợp của mô hình hồi quy tuyến tính thường dùng là hệ số xác định R2 (R square). Khi phần lớn các điểm dữ liệu tập trung sát vào đường hồi quy, giá trị R2 sẽ cao, ngược lại, nếu các điểm dữ liệu phân bố rải rác cách xa đường hồi quy, R2 sẽ thấp.
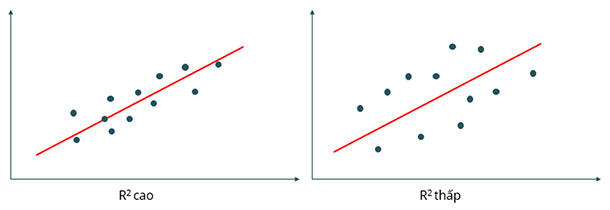
Hệ số R bình phương được chứng mình là hàm không giảm theo số biến độc lập được đưa vào mô hình, nếu chúng ta đưa thêm càng nhiều biến độc lập vào phương trình, chỉ số R bình phương sẽ càng tăng. Việc tăng giá trị R bình phương bằng cách đưa thêm biến vào mô hình không phải lúc nào cũng là tốt, bởi có thể xảy ra nhiều vấn đề như đa cộng tuyến, biến thừa, nhiều biến phức tạp cho khâu phân tích.
2. Hệ số R2 hiệu chỉnh (Adjusted R Square ) là gì?
Khi chúng ta đưa thêm biến độc lập vào phân tích hồi quy, R2 có xu hướng tăng lên. Điều này dẫn đến một số trường hợp mức độ phù hợp của mô hình hồi quy bị thổi phồng khi chúng ta đưa vào các biến độc lập giải thích rất yếu hoặc không giải thích cho biến phụ thuộc. Trong SPSS, bên cạnh chỉ số R2, chúng ta còn có thêm chỉ số R2 Adjusted (R2 hiệu chỉnh). Chỉ số R2 hiệu chỉnh không nhất thiết tăng lên khi nhiều biến độc lập được thêm vào hồi quy, do đó R2 hiệu chỉnh phản ánh độ phù hợp của mô hình chính xác hơn hệ số R2.
Cả hai giá trị R bình phương (R Square) và R bình phương hiệu chỉnh (Adjusted R Square) nằm trong bảng Coefficients trong kết quả phân tích hồi quy tuyến tính trên SPSS. R bình phương hiệu chỉnh luôn nhỏ hơn hoặc bằng R bình phương.
3. Ngưỡng và ý nghĩa của R2 (R bình phương)
R2 hay R2 hiệu chỉnh đều có mức dao động trong đoạn từ 0 đến 1. Nếu R2 càng tiến về 1, các biến độc lập giải thích càng nhiều cho biến phụ thuộc, và ngược lại, R2 càng tiến về 0, các biến độc lập giải thích càng ít cho biến phụ thuộc. Ví dụ, một mô hình hồi quy với biến phụ thuộc Y và hai biến độc lập: X1, X2 cho ra giá trị R2 hiệu chỉnh là 0.40. Điều này có nghĩa, hai biến độc lập đưa vào phân tích hồi quy giải thích được 40% sự biến thiên của biến phụ thuộc, 60% còn lại được giải thích bởi phần dư gồm các biến độc lập ngoài mô hình và sai số ngẫu nhiên.
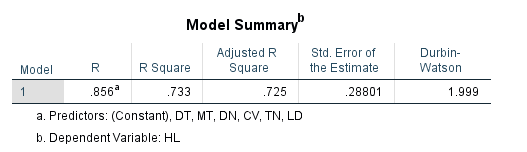
Trong ví dụ đọc kết quả hồi quy trên SPSS ở trên, giá trị R bình phương hiệu chỉnh là 0.725. Như vậy, các biến độc lập giải thích được 72.5% sự biến thiên của biến phụ thuộc. Phần còn lại 27.5% được giải thích bởi các biến ngoài mô hình và sai số ngẫu nhiên.
4. R bình phương hiệu chỉnh dưới 50% (dưới 0.5)
Không có tiêu chuẩn chính xác R2 ở mức bao nhiêu thì mô hình mới đạt yêu cầu. Mặc dù có một số nhà nghiên cứu đã cố gắng đề xuất các ngưỡng chấp nhận của chỉ số này nhưng chúng chỉ áp dụng ở một số trường hợp cụ thể.
Cần lưu ý rằng, không phải luôn luôn một mô hình hồi quy có R2 cao thì nghiên cứu có giá trị cao, mô hình có R2 thấp thì nghiên cứu đó có giá trị thấp, độ phù hợp mô hình hồi quy không có mối quan hệ nhân quả với giá trị của bài nghiên cứu. Trong nghiên cứu lặp lại, chúng ta thường chọn mức trung gian là 0.5 để phân ra 2 nhánh ý nghĩa mạnh/ý nghĩa yếu và kỳ vọng từ 0.5 đến 1 thì mô hình là tốt, bé hơn 0.5 là mô hình chưa tốt. Tuy nhiên, điều này không thực sự chính xác bởi việc đánh giá giá trị R2 sẽ phụ thuộc rất nhiều vào các yếu tố như lĩnh vực nghiên cứu, tính chất nghiên cứu, cỡ mẫu, số lượng biến tham gia hồi quy, kết quả các chỉ số khác của phép hồi quy,…
