Phân tích nhân tố khám phá EFA đối với mô hình biến bậc hai có những đặc thù khác biệt đáng kể so với mô hình chỉ bao gồm các biến bậc một. Những khác biệt này thể hiện cả ở cách tiếp cận phương pháp lẫn kỳ vọng về cấu trúc nhân tố thu được từ kết quả phân tích. Trong bài viết này, nội dung sẽ tập trung trình bày chi tiết hai dạng mô hình biến bậc hai, tương ứng với hai cách tiếp cận và hai nhóm kỳ vọng khác nhau đối với kết quả EFA.
Trước khi đi sâu vào nội dung chính, cần nhắc lại một số khái niệm nền tảng liên quan đến giá trị hội tụ và giá trị phân biệt của các nhân tố, được thể hiện thông qua ma trận xoay trong phân tích EFA.
– Giá trị hội tụ phản ánh mức độ mà các biến quan sát có cùng bản chất và cùng đo lường một khái niệm tiềm ẩn sẽ tập trung tải mạnh lên cùng một nhân tố. Xét trên góc độ dữ liệu, hiện tượng hội tụ xảy ra khi các biến quan sát này có mối tương quan chặt chẽ với nhau, qua đó hình thành một nhân tố đại diện.
– Giá trị phân biệt thể hiện khả năng tách biệt rõ ràng giữa các nhóm biến quan sát, trong đó mỗi nhóm tải chủ yếu lên một nhân tố riêng biệt. Về mặt thống kê, sự phân biệt giữa các nhân tố xuất hiện khi các biến trong cùng một nhân tố có mức tương quan thấp với các biến thuộc các nhân tố khác, qua đó đảm bảo tính độc lập tương đối giữa các cấu trúc tiềm ẩn.
1. Mối quan hệ giữa biến bậc hai và biến bậc một theo mô hình phản xạ (reflective)
Trong trường hợp mối quan hệ giữa biến bậc hai và các biến bậc một được mô hình hóa theo hướng phản xạ (reflective), biến bậc hai được xem là khái niệm tiềm ẩn tổng quát, còn các biến bậc một là những biểu hiện hay kết quả được sinh ra từ biến bậc hai đó. Do hướng tác động đi từ biến bậc hai đến các biến bậc một, các biến bậc một được kỳ vọng có mức độ tương quan tương đối cao với nhau. Chẳng hạn, giả định trong mô hình nghiên cứu, biến MKT tác động đến bốn biến bậc một là PP, GC, SP và KM theo mối quan hệ reflective.
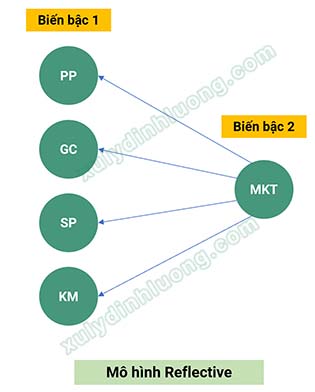
Do các biến bậc một có mức độ tương quan cao, các biến quan sát cấu thành từng biến bậc một cũng sẽ có xu hướng tương quan mạnh với nhau. Theo nguyên lý của phân tích nhân tố khám phá, khi các biến quan sát có mối tương quan đáng kể, chúng có xu hướng hội tụ vào cùng một nhân tố. Trên cơ sở đó, trong phân tích EFA, có thể kỳ vọng rằng các biến quan sát thuộc các thành phần PP, GC, SP và KM sẽ cùng tải lên một nhân tố, thể hiện qua việc nằm trong cùng một cột của ma trận xoay.
Tuy nhiên, trong một số trường hợp, một, một vài hoặc thậm chí tất cả các biến bậc một có thể tách ra thành các nhóm nhân tố riêng biệt trong kết quả EFA. Hiện tượng này được xem là bình thường và có thể xảy ra khi mức độ tương quan giữa các biến bậc một không đủ mạnh. Trong trường hợp đó, nhà nghiên cứu vẫn tiếp tục sử dụng kết quả EFA để tiến hành phân tích nhân tố khẳng định (CFA). Việc đánh giá mức độ phù hợp và ý nghĩa của các biến bậc một sẽ dựa trên các chỉ tiêu độ tin cậy và giá trị hội tụ của biến bậc hai trong mô hình CFA, bao gồm độ tin cậy tổng hợp (CR), phương sai trích trung bình (AVE) và hệ số tải chuẩn hóa của các biến bậc một.
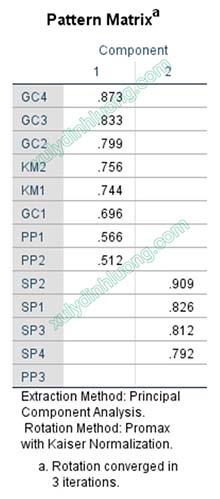
Việc xuất hiện biến bậc một tách riêng trong phân tích EFA không được xem là vấn đề nghiêm trọng. Nếu kết quả EFA khi phân tích chung toàn bộ các biến trong mô hình cho thấy cấu trúc nhân tố rõ ràng và phù hợp, nhà nghiên cứu nên giữ nguyên cách phân tích này. Ngược lại, trong trường hợp kết quả EFA cho thấy sự xáo trộn lớn, cấu trúc nhân tố không rõ ràng hoặc ma trận xoay phức tạp, việc tách riêng phân tích EFA cho biến bậc hai và phân tích EFA cho các biến còn lại trong mô hình là một lựa chọn phù hợp nhằm đảm bảo tính rõ ràng và hợp lệ của cấu trúc thang đo.
2. Mối quan hệ giữa biến bậc hai và biến bậc một theo hướng formative
Trong trường hợp mối quan hệ giữa biến bậc hai và các biến bậc một được xây dựng theo mô hình nguyên nhân formative, các biến bậc một đóng vai trò là những yếu tố tạo thành biến bậc hai. Nói cách khác, biến bậc hai được hình thành từ sự kết hợp của các biến bậc một, với chiều tác động được giả định từ biến bậc một lên biến bậc hai. Khi đó, mỗi biến bậc một đại diện cho một thành phần riêng biệt trong cấu trúc khái niệm, do vậy mức độ tương quan giữa các biến bậc một thường ở mức thấp. Ví dụ, trong mô hình minh họa, mối quan hệ từ biến MKT đến bốn biến PP, GC, SP và KM được xác định là quan hệ formative.
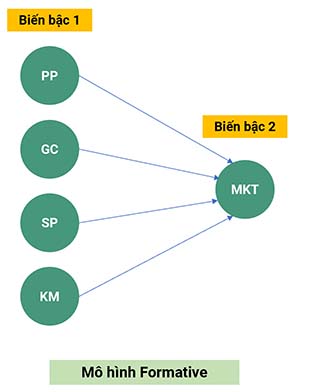
Do các biến bậc một có mức độ tương quan thấp với nhau, các biến quan sát thuộc về từng biến bậc một cũng có xu hướng tương quan yếu. Như đã trình bày ở phần trước, khi thực hiện phân tích EFA, nếu các biến quan sát có mức độ tương quan thấp, chúng sẽ được tách thành các nhân tố riêng biệt. Dựa trên đặc điểm này, kỳ vọng khi tiến hành EFA là các biến quan sát của PP, GC, SP và KM sẽ hội tụ vào các cột riêng biệt trong ma trận xoay.
Kỳ vọng kết quả EFA đối với các biến bậc một theo hướng formative tương tự như kỳ vọng EFA đối với các biến độc lập trong mô hình nghiên cứu. Khi đó, mỗi biến bậc một được xem xét như một biến độc lập riêng rẽ trong phân tích nhân tố.
Trong trường hợp kết quả EFA cho thấy sự gộp nhóm hoặc tách nhóm giữa các biến bậc một không phù hợp với cấu trúc lý thuyết ban đầu, chẳng hạn như hai biến bậc một hội tụ vào cùng một nhân tố hoặc một biến bậc một bị tách thành hai nhóm nhỏ, mô hình biến bậc một cần được điều chỉnh lại. Việc điều chỉnh bao gồm xác định lại cấu trúc thành phần, đặt tên các biến bậc một mới và tiếp tục xử lý theo quy trình phân tích thông thường.
Tình huống gộp hoặc tách các biến bậc một so với cấu trúc lý thuyết có bản chất tương tự như việc gộp hoặc tách các biến độc lập trong nghiên cứu. Do đó, cách thức xử lý EFA đối với các biến bậc một formative cũng tương tự như cách xử lý EFA đối với các biến độc lập.
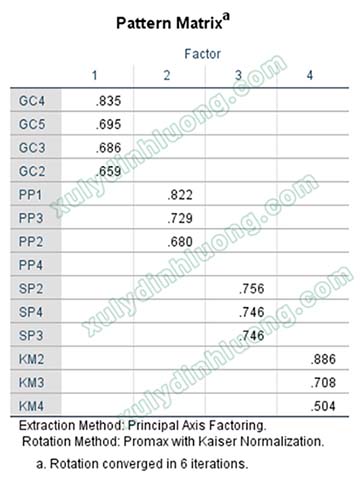
Trong trường hợp kết quả EFA khi chạy chung toàn bộ các biến trong mô hình cho thấy cấu trúc rõ ràng và phù hợp, việc phân tích chung là lựa chọn ưu tiên. Tuy nhiên, nếu xuất hiện nhiều sự xáo trộn, ma trận xoay không rõ ràng hoặc khó diễn giải, cần xem xét tách riêng việc chạy EFA cho nhóm biến thuộc biến bậc hai và chạy EFA riêng cho các biến còn lại trong mô hình.
