Trong phân tích thống kê, Skewness (độ lệch) và Kurtosis (độ nhọn) là hai chỉ số then chốt được sử dụng để đánh giá mức độ mà dữ liệu tuân theo phân phối chuẩn (Normal Distribution) khi xử lý và phân tích bằng phần mềm SPSS.
1. Chỉ số độ lệch Skewness
a. Khái niệm về độ lệch Skewness
Skewness là một chỉ số thống kê mô tả phản ánh mức độ bất đối xứng của phân phối dữ liệu. Chỉ số này cho biết dữ liệu có xu hướng phân bố lệch về phía bên trái hay bên phải so với giá trị trung bình của biến quan sát.
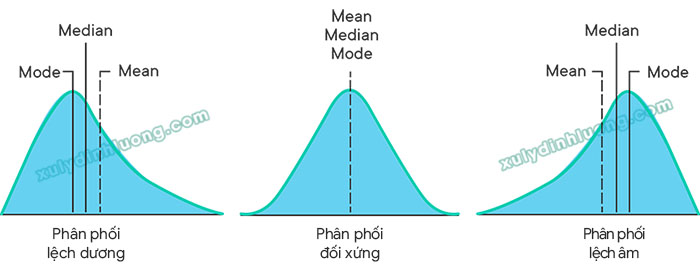
Về mặt hình thái, độ lệch của phân phối dữ liệu có thể được khái quát thành ba dạng cơ bản:
Skewness > 0 (Mean > Median): Đây là dạng phân phối lệch dương, còn gọi là phân phối lệch phải. Trong trường hợp này, phần đuôi bên phải của phân phối kéo dài hơn so với bên trái, cho thấy sự xuất hiện của một số giá trị lớn bất thường. Dạng phân phối này thường không đáp ứng giả định phân phối chuẩn.
Skewness = 0 (Mean = Median = Mode): Đây là dạng phân phối đối xứng. Phần đuôi hai bên của phân phối tương đối cân bằng và đối xứng quanh giá trị trung tâm, phản ánh đặc trưng của phân phối chuẩn.
Skewness < 0 (Mean < Median): Đây là dạng phân phối lệch âm, hay phân phối lệch trái. Phần đuôi bên trái của phân phối kéo dài hơn so với bên phải, cho thấy sự tập trung của các giá trị lớn hơn mức trung bình. Phân phối này thường không thỏa mãn điều kiện phân phối chuẩn.
b. Đánh giá phân phối chuẩn dựa trên độ lệch Skewness
Chỉ số Skewness được sử dụng để đánh giá mức độ đối xứng của phân phối dữ liệu của một biến nghiên cứu. Khi phân phối có xu hướng kéo dài về một phía của trục giá trị, phân phối đó được xem là bị lệch. Độ lệch âm cho thấy dữ liệu tập trung nhiều ở phía giá trị lớn hơn trung bình, trong khi độ lệch dương phản ánh sự tập trung của các giá trị nhỏ hơn trung bình.
Theo Hair và cộng sự (2022), việc đánh giá phân phối chuẩn của dữ liệu dựa trên chỉ số Skewness có thể được xác định theo các ngưỡng sau:
- Skewness nằm trong khoảng từ -1 đến 1 được xem là mức lý tưởng để kết luận dữ liệu có phân phối chuẩn.
- Skewness nằm trong khoảng từ -2 đến 2 được chấp nhận để kết luận dữ liệu có phân phối chuẩn.
- Skewness vượt ra ngoài khoảng từ -2 đến 2 cho thấy dữ liệu không tuân theo phân phối chuẩn.
2. Chỉ số độ nhọn Kurtosis
a. Khái niệm độ nhọn Kurtosis
Kurtosis (độ nhọn) là một chỉ số thống kê mô tả dùng để phản ánh đặc điểm hình dạng của phân phối dữ liệu, thông qua mức độ nhọn của đỉnh phân phối và mức độ dày của phần đuôi. Phân phối có giá trị kurtosis cao cho thấy dữ liệu tập trung nhiều ở phần trung tâm và có các đuôi dày. Ngược lại, phân phối có giá trị kurtosis thấp thể hiện dữ liệu phân tán nhiều hơn và đỉnh phân phối tương đối bẹt.
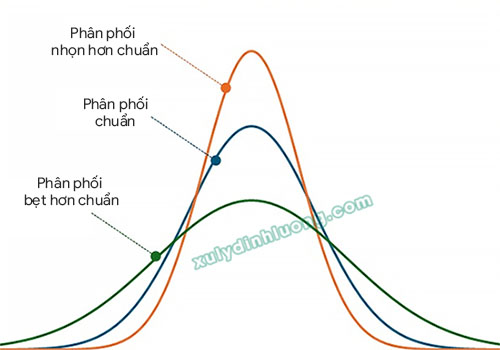
Theo định nghĩa ban đầu, phân phối chuẩn có giá trị kurtosis bằng 3. Tuy nhiên, trong nhiều tài liệu nghiên cứu, giáo trình và các phần mềm thống kê, trong đó có SPSS, chỉ số kurtosis thường được hiệu chỉnh về mốc 0 nhằm thuận tiện cho việc diễn giải. Giá trị kurtosis sau khi hiệu chỉnh này được gọi là Excess Kurtosis (độ nhọn dư), được xác định theo công thức Excess Kurtosis = Kurtosis − 3.
Trong phần mềm SPSS, mặc dù thuật ngữ hiển thị là Kurtosis, nhưng giá trị được báo cáo thực chất là Excess Kurtosis. Vì vậy, khi phân tích kết quả từ SPSS, giá trị kurtosis cần được so sánh với mốc 0 thay vì mốc 3 như trong định nghĩa ban đầu.
Xét tổng quát, hình dạng phân phối theo độ nhọn có thể được phân thành ba dạng cơ bản:
- Excess Kurtosis > 0: Phân phối nhọn hơn phân phối chuẩn (Leptokurtic), đặc trưng bởi đỉnh cao và nhọn.
- Excess Kurtosis = 0: Phân phối chuẩn (Mesokurtic), có mức độ nhọn trung bình.
- Excess Kurtosis < 0: Phân phối bẹt hơn phân phối chuẩn (Platykurtic), với đỉnh rộng và thấp.
b. Đánh giá phân phối chuẩn dựa trên độ nhọn Kurtosis
Độ nhọn Kurtosis phản ánh mức độ phân phối dữ liệu có nhọn hoặc bẹt hơn so với phân phối chuẩn. Giá trị kurtosis dương cho thấy phân phối có đỉnh cao hơn và đuôi dày hơn, trong khi giá trị kurtosis âm cho thấy phân phối phẳng hơn và dữ liệu phân tán nhiều hơn.
Theo Hair và cộng sự (2022), việc đánh giá phân phối chuẩn của dữ liệu dựa trên chỉ số Kurtosis (đã được hiệu chỉnh bằng cách trừ đi 3) có thể căn cứ theo các ngưỡng sau:
- Kurtosis xấp xỉ 0: mức lý tưởng để kết luận dữ liệu có phân phối chuẩn;
- Kurtosis nằm trong khoảng từ −2 đến 2: mức chấp nhận được để xem dữ liệu có phân phối chuẩn;
- Kurtosis vượt ra ngoài khoảng từ −2 đến 2: dữ liệu không thỏa mãn giả định phân phối chuẩn.
3. Quy trình tính toán chỉ số Skewness và Kurtosis trong SPSS
Để xác định các chỉ số Skewness và Kurtosis trong phần mềm SPSS, người nghiên cứu thực hiện thao tác tương tự như khi tiến hành thống kê mô tả cho giá trị trung bình. Trên giao diện chính của SPSS, chọn Analyze, sau đó vào Descriptive Statistics và tiếp tục chọn Descriptives.
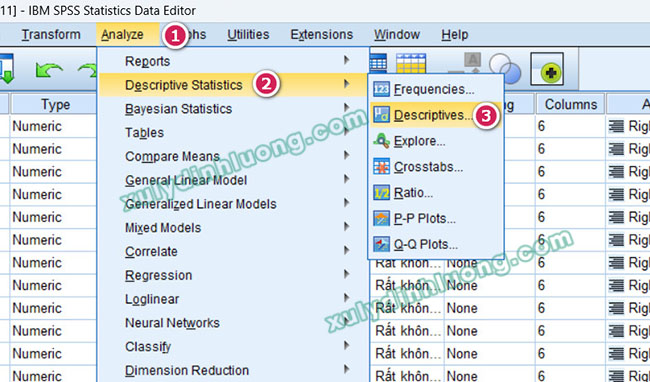
Khi hộp thoại Descriptives xuất hiện, các biến cần kiểm tra độ lệch và độ nhọn của phân phối được đưa vào mục Variable(s). Tiếp theo, người dùng lựa chọn nút Options để thiết lập các tham số thống kê cần xuất.
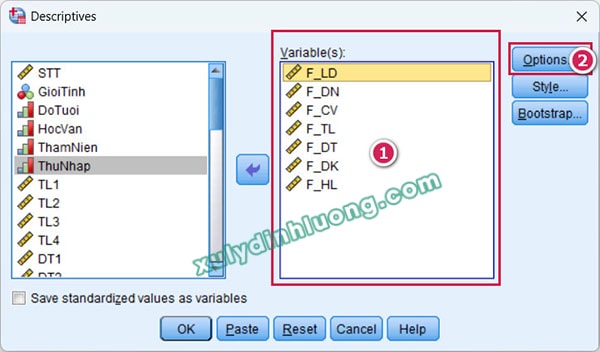
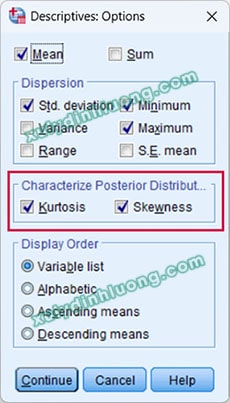
Trong cửa sổ Options, tiến hành đánh dấu chọn hai chỉ tiêu Skewness và Kurtosis. Sau đó nhấn Continue để quay lại giao diện Descriptives ban đầu và chọn OK nhằm hiển thị kết quả phân tích trong cửa sổ Output.
SPSS sẽ cung cấp giá trị của hai chỉ số Skewness và Kurtosis trong bảng Descriptive Statistics, thể hiện đặc điểm phân phối của các biến nghiên cứu.
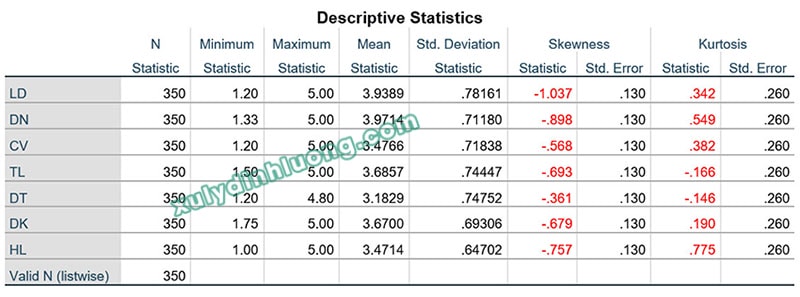
→ Kết quả cho thấy các giá trị Skewness và Kurtosis của các biến đều nằm trong khoảng từ -2 đến 2, qua đó có thể kết luận rằng dữ liệu của các biến này có phân phối xấp xỉ phân phối chuẩn.
Lưu ý:
Việc đánh giá mức độ phân phối chuẩn của dữ liệu không nên chỉ dựa trên một tiêu chí đơn lẻ mà cần kết hợp đồng thời nhiều phương pháp khác nhau, bao gồm giá trị Skewness và Kurtosis, đồ thị P-P Plot, đồ thị Q-Q Plot, biểu đồ Histogram, cũng như các kiểm định thống kê như Shapiro-Wilk và Kolmogorov-Smirnov, nhằm đảm bảo độ chính xác và tin cậy của kết luận nghiên cứu.
———-
Nguồn tham khảo:
Hair và cộng sự (2022). A Primer on Partial Least Squares Structural Equation Modeling (PLS-SEM) (3 ed.). Thousand Oaks, CA: Sage.
